当机器学习模型过拟合时,可以采用正则化(Regularization)方法。
正则化原理
假设机器学习算法的损失函数如下(具体概念请见之前的文章):
$$\begin{align} J(w) = {\frac 1 m} \sum _{i=1}^m L(\hat y^{(i)}, y^{(i)}) \end{align}$$L2 正则化
L2 正则化即在损失函数后加入 L2泛数:
$$\begin{align} ||w||_2 & = \sqrt {\sum_{i=1}^m w_i^2} \\ J_{L2}(w) & = {\frac 1 m} \sum _{i=1}^m L(\hat y^{(i)}, y^{(i)}) + {\frac {\lambda} {2m}} ||w||_2^2 \end{align}$$L1 正则化
L1 正则化即在损失函数后加入 L1泛数:
$$\begin{align} ||w||_1 & = \sum_{i=1}^m |w_1| \\ J_{L1}(w) & = {\frac 1 m} \sum _{i=1}^m L(\hat y^{(i)}, y^{(i)}) + {\frac {\lambda} m} ||w||_1 \end{align}$$正则化的图形解释
以 Adaline 为例(其代价函数为圆形,容易绘制),从图形角度解释正则化的原因。
假设有两个权重 $w_1$ 和 $w_2$,其损失函数为凸函数,如下图,
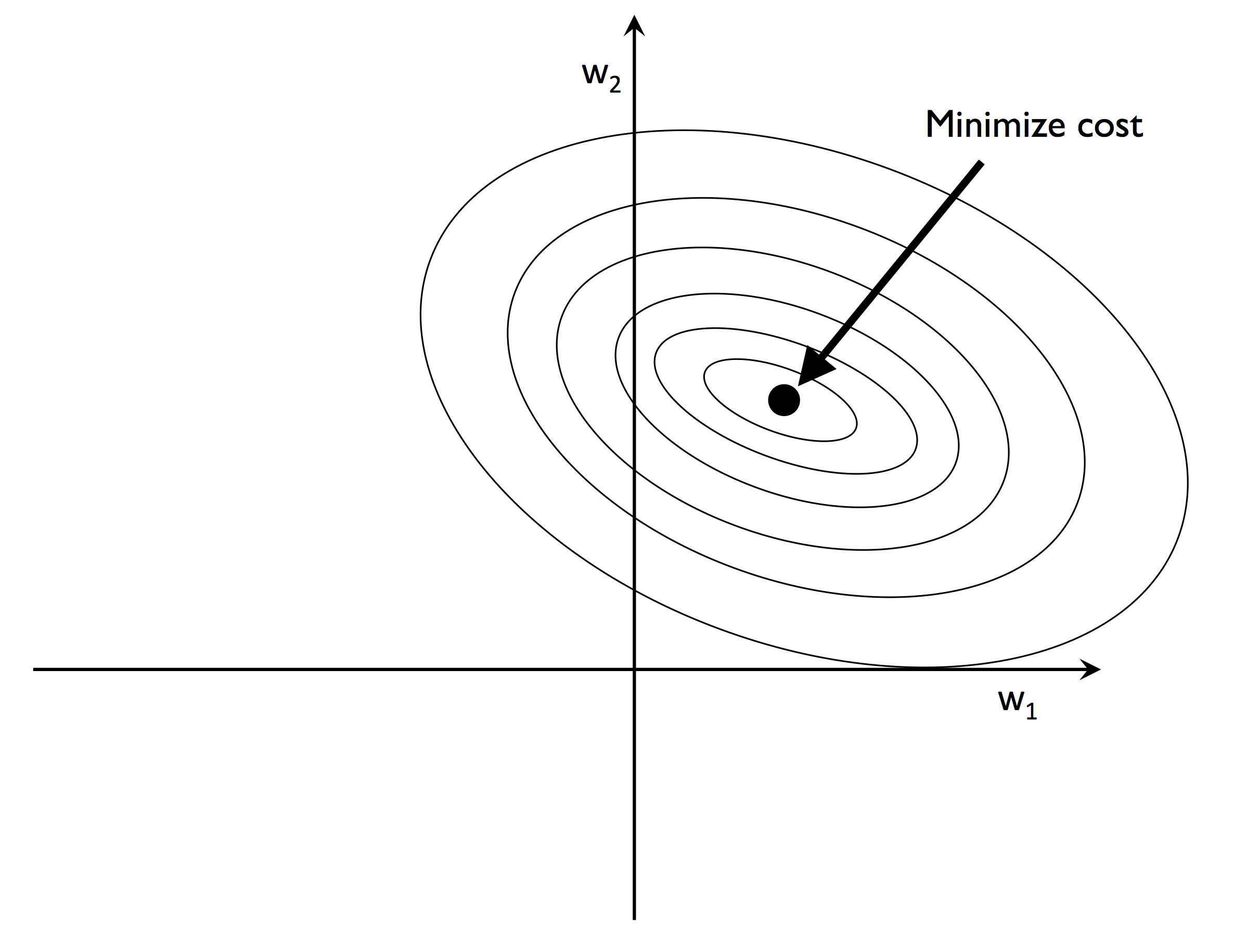
L2 正则化的结果如下:
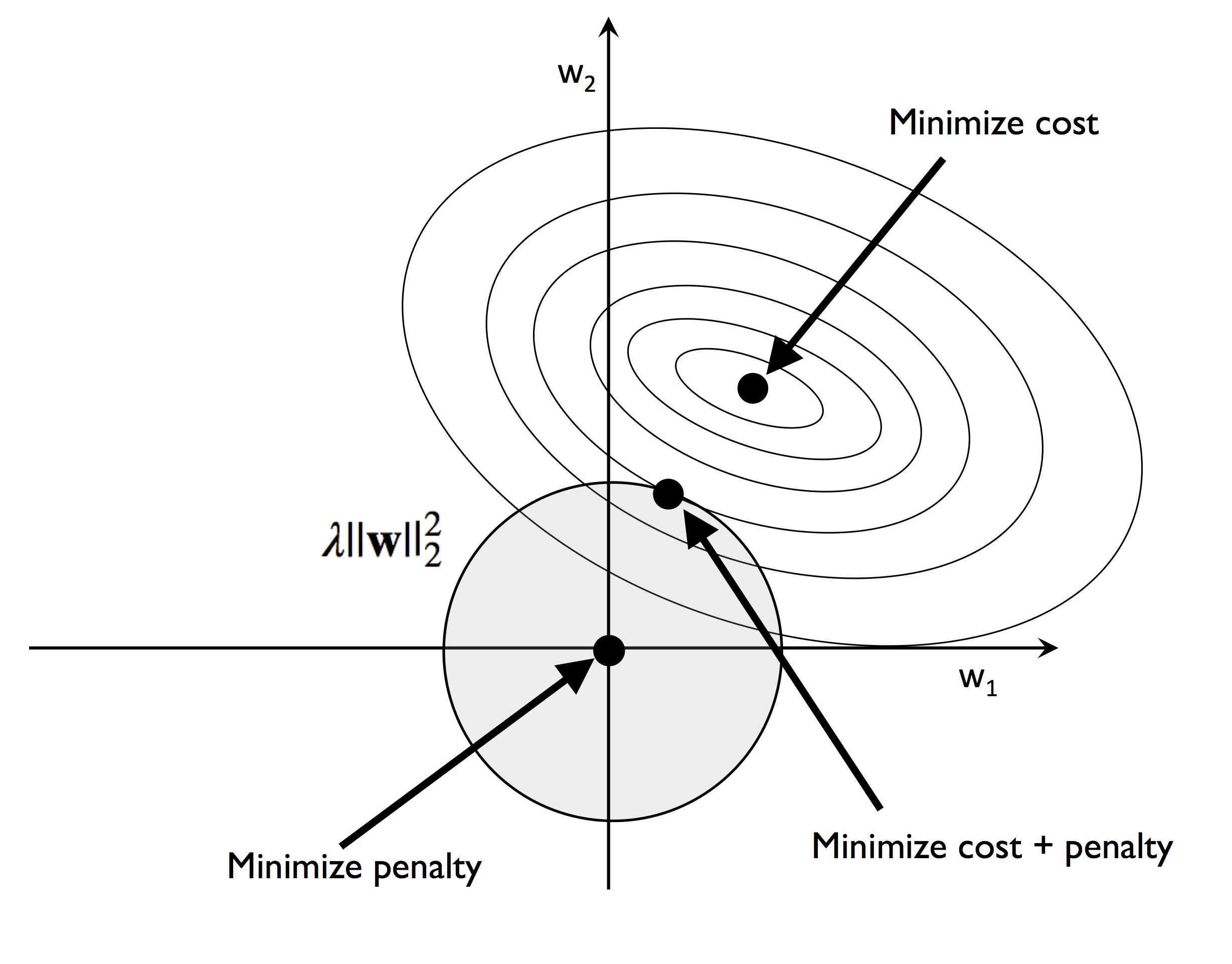
L2 泛数为惩罚项,在 L2 泛数不能超过阴影圆所示区域的基础上,希望最小化成本函数。由于惩罚项不能超过一定值,若 $\lambda$ 越大,则 $||w||_2$ 的范围越小。
L1 正则化的结果如下:
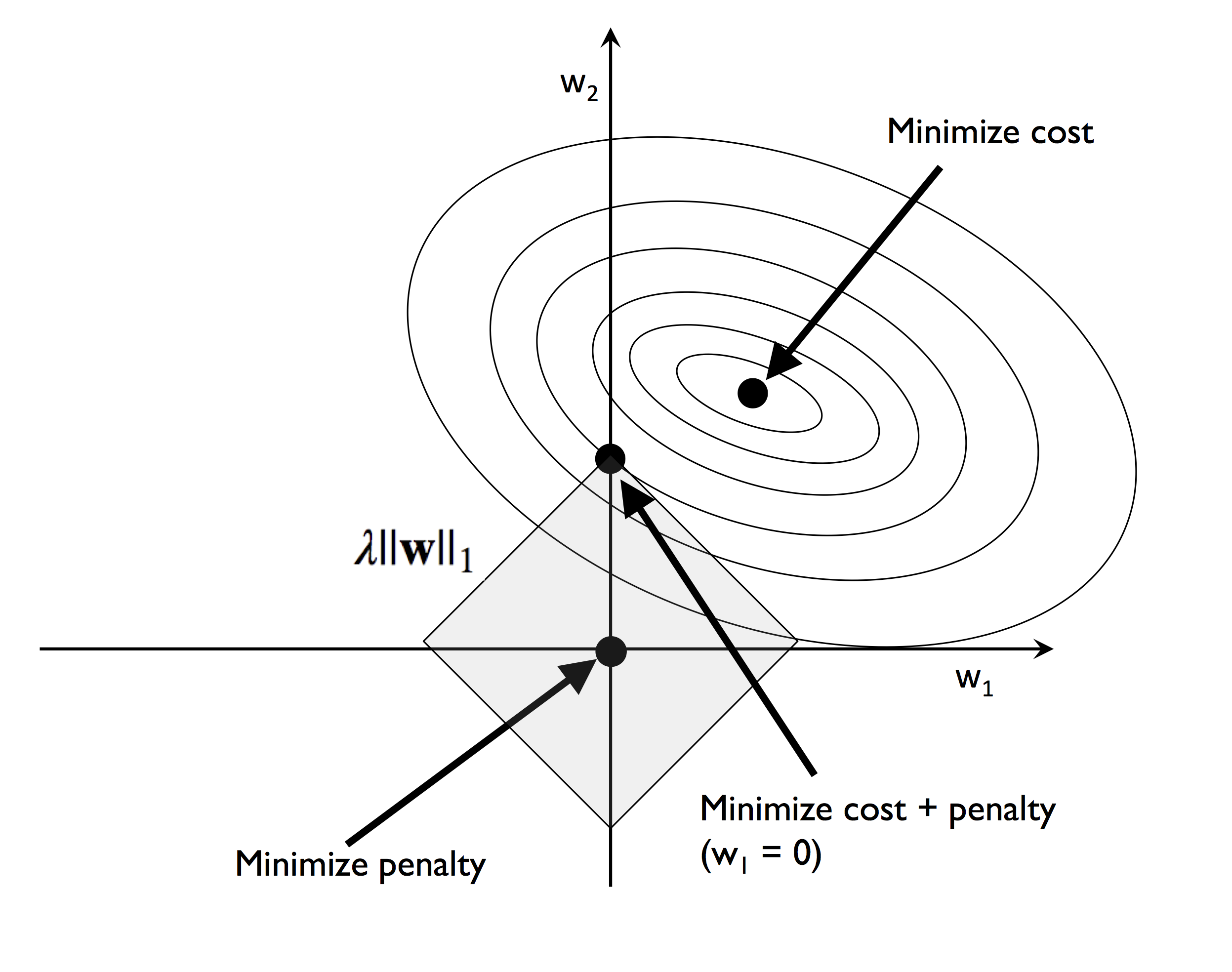
L1 类似于 L2,区别是 L1 泛数的区域为所示正方形,最小化成本函数时往往会出现部分权重退化为 0 的情况,也就是说稀疏了一部分权重。
正则化的数学解释
以梯度下降法进行说明 L2 正则化后的权重更新:
$$\begin{align} \frac {\partial J_{L2}} {\partial w} & = \frac {\partial J} {\partial w} + \frac \lambda m w_i \\ w_i & := w_i - \alpha \frac {\partial J_{L2}} {\partial w} = (1 - \alpha {\frac \lambda m}) w_i - \alpha \frac {\partial J} {\partial w} \end{align}$$与未添加正则化的公式相比,L2 正则化每一次迭代后权重都要乘以一个小于 1 的因子,因此权重可以不断减小。