线性判别分析

发表于 | 分类于

线性判别分析（Linear Discriminant Analysis，LDA）作为一种特征提取技术，可以提高计算效率，防止由于维数灾难而导致的过拟合。
LDA 与 PCA 类似，不同之处在于 PCA 的目标是找到数据集中最大方差的正交分量轴，而 LDA 的目标是找到优化类可分性的特征子空间。

LDA 和 PCA 都是线性变换技术，可用于减少数据集中的维数。区别在于 LDA 是监督算法，而 PCA 是无监督算法。

LDA 旨在找到对应最多投影的线性判别，如下图所示，其中圆形和十字分别表示两类的正态分布样本：

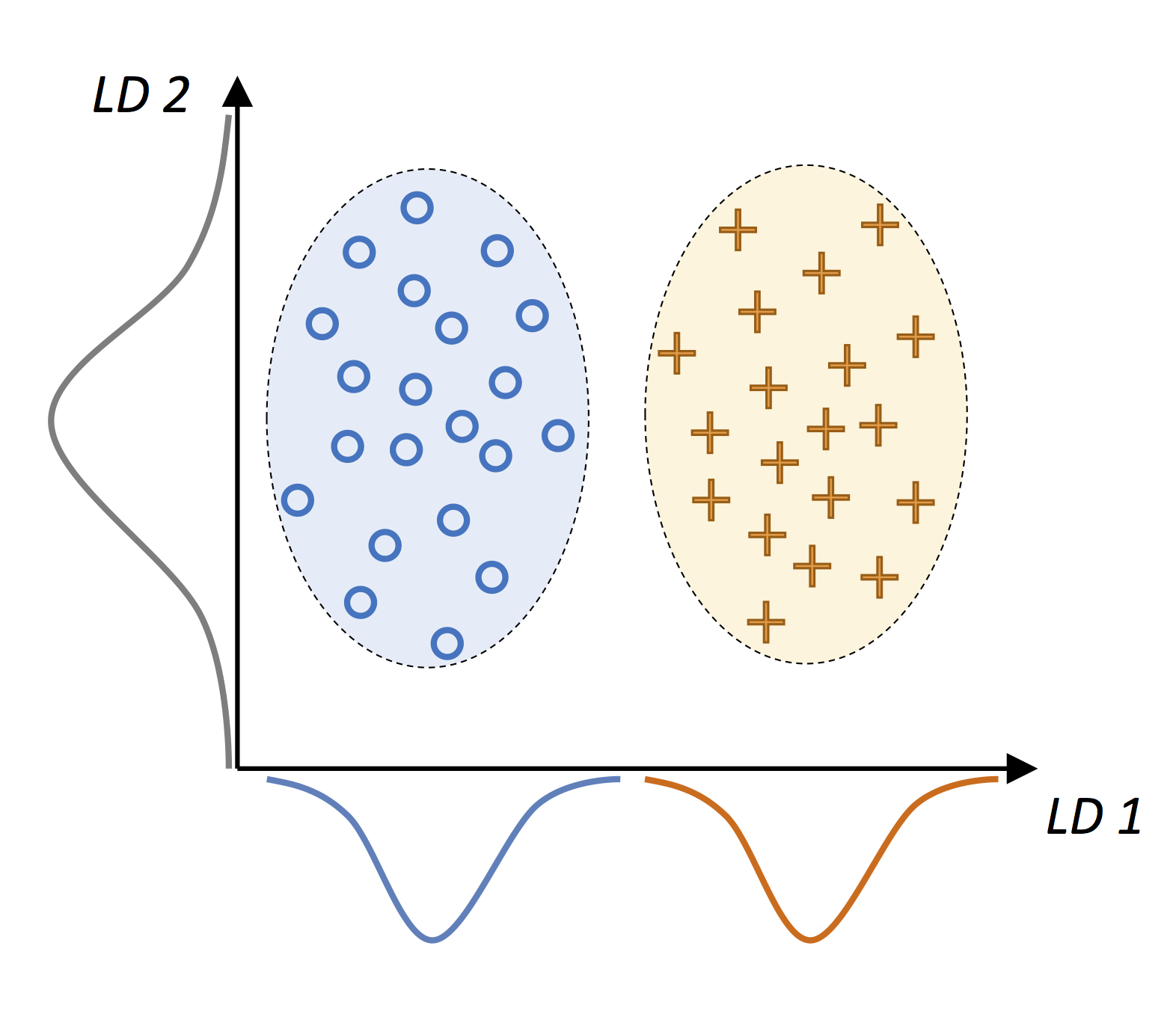
$x$ 轴（LD1）所示的线性判别可以很好地分类；而尽管 $y$ 轴（LD2）所示的线性判别拥有更大的投影方差，但是无法捕获任何分类信息。

LDA 中假设数据是正态分布的。此外，我们假设类的协方差矩阵相同，并且特征之间互不相关。

算法思想

LDA 的算法流程的简单介绍如下：

  1. 对输入的 $d$ 维数据集 $\boldsymbol X$ 进行标准化。
  2. 计算每个类的 $d$ 维均值向量，构造类内散布矩阵 $\boldsymbol S_W$ 和类间散布矩阵 $\boldsymbol S_B$。
  3. 计算矩阵 $\boldsymbol S_W^{-1} \boldsymbol S_B$ 的特征向量和特征值。
  4. 对特征值进行降序排序，对相应的特征向量进行排序。
  5. 提取 $k$ 个最大特征值对应的特征向量，其中 $k$ ($k \le d$) 是新特征子空间的维数。
  6. 使用提取的 $k$ 个特征向量构造投影矩阵 $\boldsymbol W$。
  7. 使用投影矩阵 $\boldsymbol W$ 对 $\boldsymbol X$ 进行变换，得到新的 $k$ 维特征子空间。

LDA 与 PCA 非常相似，通过将矩阵分解成特征值和特征向量，然后通过投影矩阵得到新的低维特征空间。其不同点在于 LDA 将类标签考虑在内（步骤 2）。

数据导入和标准化

导入 Wine 数据集 ，第 1 列为其分类标签，第 2~14 列为特征。分割数据集为 70% 的训练集和 30% 的测试集：

1
2
3
4
5
6
import pandas as pd
from sklearn.model_selection import train_test_split

df_wine = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data', header=None)
X, y = df_wine.iloc[:, 1:].values, df_wine.iloc[:, 0].values
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0, stratify=y)

对训练集和测试集进行标准化：

1
2
3
4
5
6
from sklearn.preprocessing import StandardScaler

sc = StandardScaler()
sc.fit(X_train)
X_train_std = sc.transform(X_train)
X_test_std = sc.transform(X_test)

散布矩阵的构造

均值向量

计算均值向量，后面将用它来构造类内散布矩阵和类间散布矩阵。在第 $i$ 类样本的均值向量为 $\boldsymbol m_i$中，存储了该类样本特征的平均值 $\mu_m$：

$$\begin{align} \boldsymbol m_i = \frac 1 {n_i} \sum_{x \in D_i}^c \boldsymbol x_m \end{align}$$

得到三个均值向量：

$$\begin{align} \boldsymbol m_i = \begin{bmatrix} \mu_{i,alcohol} \\ \mu_{i,malic \ acid} \\ \vdots \\ \mu_{i,proline} \end{bmatrix} \end{align}$$ 
1
2
3
4
5
6
7
8
9
10
11
12
np.set_printoptions(precision=4)
mean_vecs = []
for label in range(1,4):
    mean_vecs.append(np.mean(X_train_std[y_train==label], axis=0))
    print('MV {}: {}\n'.format(label, mean_vecs[label-1]))
# Output:
# MV 1: [ 0.9066 -0.3497  0.3201 -0.7189  0.5056  0.8807  0.9589 -0.5516  0.5416
#   0.2338  0.5897  0.6563  1.2075]
# MV 2: [-0.8749 -0.2848 -0.3735  0.3157 -0.3848 -0.0433  0.0635 -0.0946  0.0703
#  -0.8286  0.3144  0.3608 -0.7253]
# MV 3: [ 0.1992  0.866   0.1682  0.4148 -0.0451 -1.0286 -1.2876  0.8287 -0.7795
#   0.9649 -1.209  -1.3622 -0.4013]

类内散布矩阵

类内散布矩阵 $\boldsymbol S_W$ 的计算如下，其中 $\boldsymbol S_i$ 为第 $i$ 类的散布矩阵。

$$\begin{align} \boldsymbol S_W & = \sum_{i=1}^c \boldsymbol S_i \\ \boldsymbol S_i & := \frac 1 {n_i} \boldsymbol S_i = \frac 1 {n_i} \sum_{x \in D_i}^c (\boldsymbol x - \boldsymbol m_i) (\boldsymbol x - \boldsymbol m_i)^T = \boldsymbol \Sigma_i \end{align}$$

由于 LDA 假设是训练集中的类别标签是均匀分布的，这里将散列矩阵 $\boldsymbol S_i$ 缩放至 $\frac 1 {n_i}$，缩放后恰好为协方差矩阵。

1
2
3
4
5
6
7
d = 13 # number of features
S_W = np.zeros((d, d))
for label,mv in zip(range(1, 4), mean_vecs):
    class_scatter = np.cov(X_train_std[y_train==label].T)
    S_W += class_scatter
print('Scaled within-class scatter matrix: {}x{}'.format(S_W.shape[0], S_W.shape[1]))
# Output: Scaled within-class scatter matrix: 13x13

类间散布矩阵

类间散布矩阵 $\boldsymbol S_B$ 的计算如下，其中 $\boldsymbol m$ 为所有样本的均值向量：

$$\begin{align} \boldsymbol S_B = \sum_{i=1}^cn_i (\boldsymbol m_i - \boldsymbol m) (\boldsymbol m_i - \boldsymbol m)^T \end{align}$$ 
1
2
3
4
5
6
7
8
9
10
mean_overall = np.mean(X_train_std, axis=0)
d = 13  # number of features
S_B = np.zeros((d, d))
for i, mean_vec in enumerate(mean_vecs):
    n = X_train[y_train == i + 1, :].shape[0]
    mean_vec = mean_vec.reshape(d, 1)  # make column vector
    mean_overall = mean_overall.reshape(d, 1)
    S_B += n * (mean_vec - mean_overall).dot((mean_vec - mean_overall).T)
print('Between-class scatter matrix: {}x{}'.format(S_B.shape[0], S_B.shape[1]))
# Output: Between-class scatter matrix: 13x13

特征值和特征向量

计算矩阵 $\boldsymbol S_W^{-1} \boldsymbol S_B$ 的特征值和特征向量，按照特征值降序对相应的特征向量进行排序：

1
2
3
eigen_vals, eigen_vecs = np.linalg.eig(np.linalg.inv(S_W).dot(S_B))
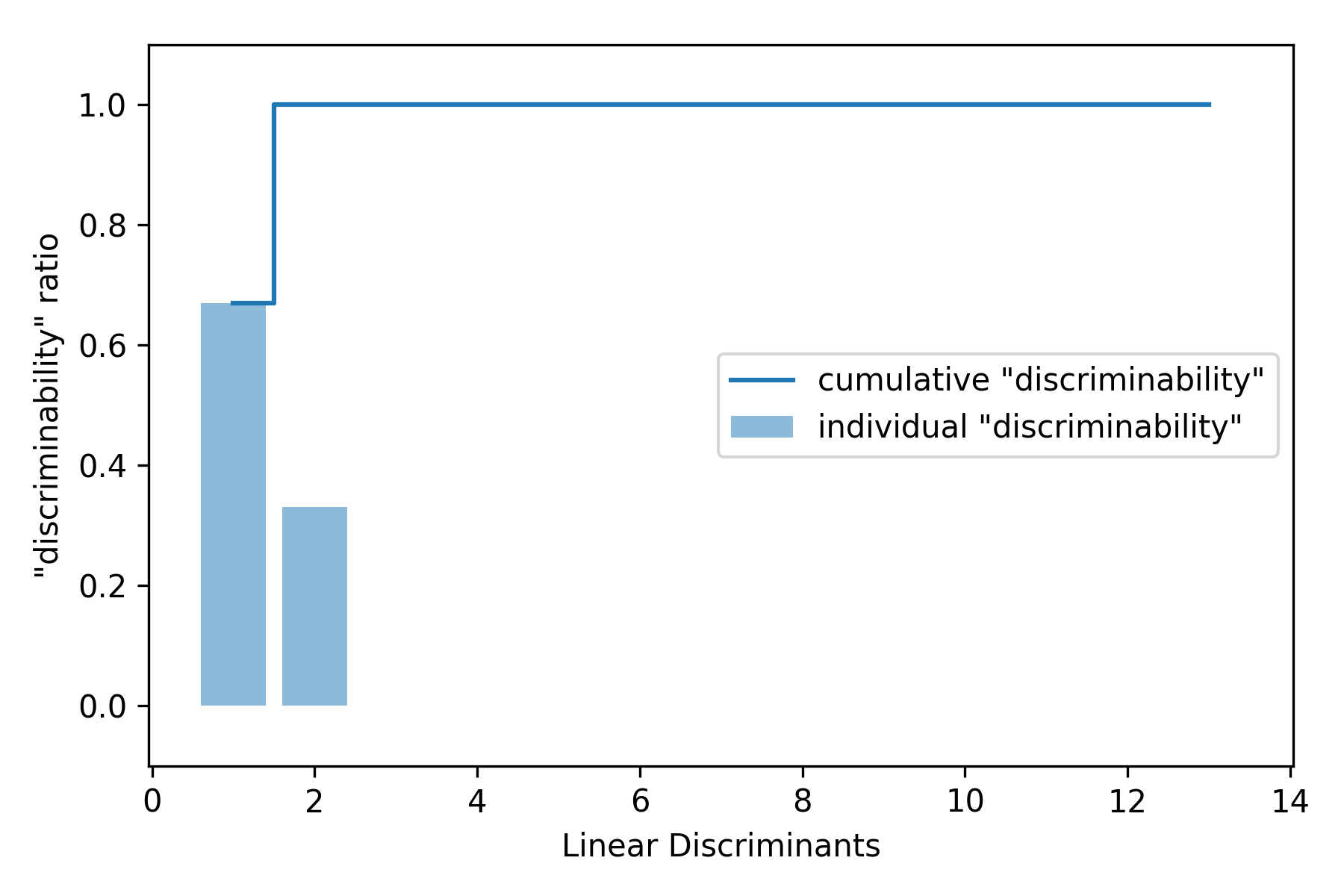
eigen_pairs = [(np.abs(eigen_vals[i]), eigen_vecs[:, i]) for i in range(len(eigen_vals))]
eigen_pairs.sort(key=lambda k: k[0], reverse=True)

在 LDA 中，线性判别式的数目至多为 $c-1$，其中 $c$ 为类标签的数量。

线性判别式的辨别能力

为了衡量线性判别式（特征向量）捕获多少类别鉴别信息，对不同的线性判别式的辨别能力（discriminability）进行绘图：

1
2
3
4
5
6
7
8
9
10
11
12
13
import matplotlib.pyplot as plt

tot = sum(eigen_vals.real)
discr = [(i / tot) for i in sorted(eigen_vals.real, reverse=True)]
cum_discr = np.cumsum(discr)

plt.bar(range(1, 14), discr, alpha=0.5, align='center', label='individual "discriminability"')
plt.step(range(1, 14), cum_discr, where='mid', label='cumulative "discriminability"')
plt.ylabel('"discriminability" ratio')
plt.xlabel('Linear Discriminants')
plt.ylim([-0.1, 1.1])
plt.legend(loc='best')
plt.show()

特征提取

使用投影矩阵转换原始数据集：

$$\begin{align} \boldsymbol x' & = \boldsymbol x \boldsymbol W \\ & \downarrow \\ \boldsymbol X' & = \boldsymbol X \boldsymbol W \end{align}$$ 
1
2
3
4
5
6
7
8
9
10
w = np.hstack((eigen_pairs[0][1][:, np.newaxis].real, eigen_pairs[1][1][:, np.newaxis].real))
X_train_lda = X_train_std.dot(w)
colors = ['r', 'b', 'g']
markers = ['s', 'x', 'o']
for l, c, m in zip(np.unique(y_train), colors, markers):
    plt.scatter(X_train_lda[y_train == l, 0], X_train_lda[y_train == l, 1] * (-1), c=c, label=l, marker=m)
plt.xlabel('LD 1')
plt.ylabel('LD 2')
plt.legend(loc='lower right')
plt.show()

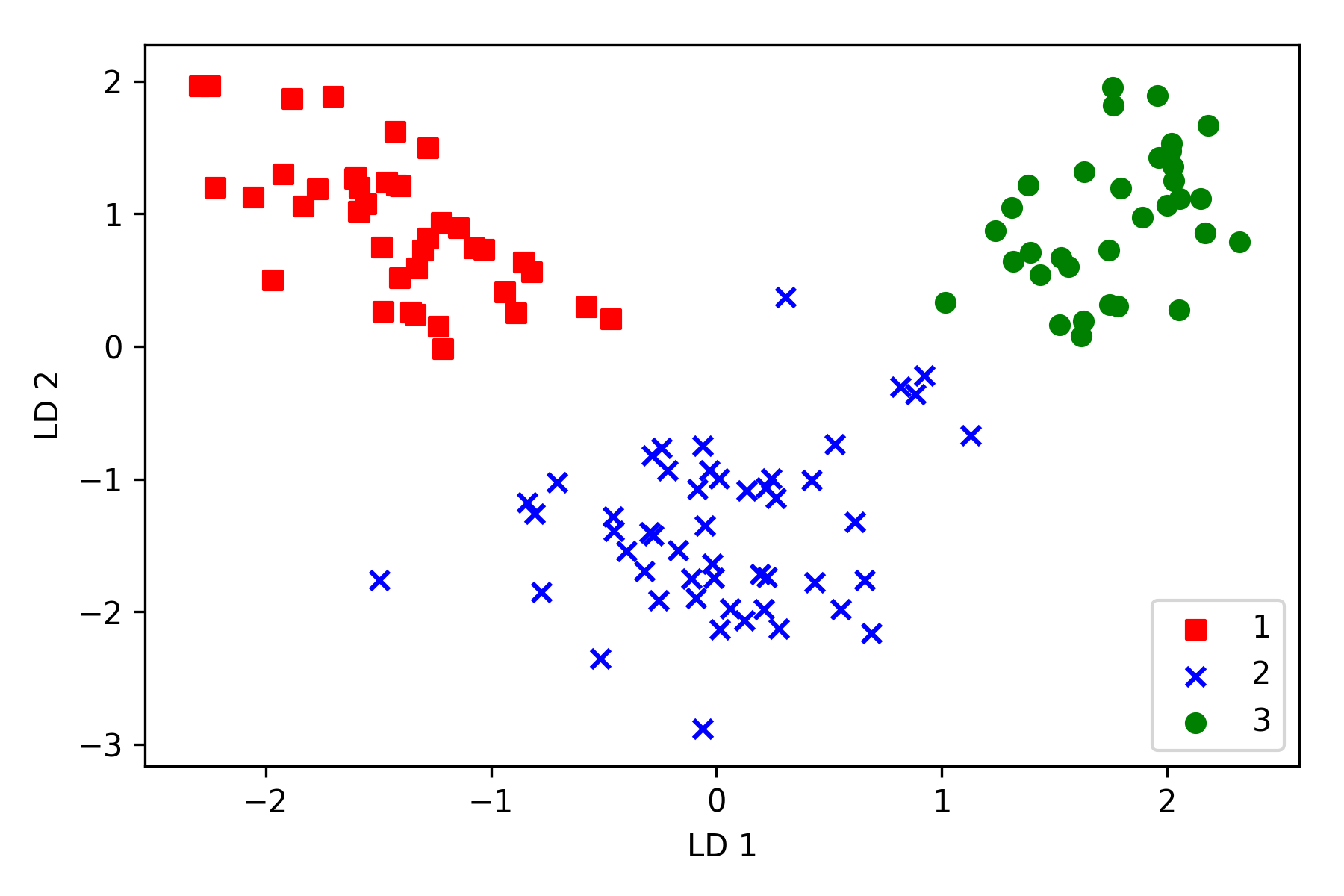
代码绘图结果如下，类别在新的特征子空间中线性可分：

Scikit-learn 实现

边界绘图函数 plot_decision_regions 见之前的文章。

通过 sklearn.discriminant_analysis.LinearDiscriminantAnalysis 将测试集和训练集降至二维，然后使用逻辑回归对降维后的测试集进行线性分类：

1
2
3
4
5
6
7
8
9
10
11
12
13
from sklearn.linear_model import LogisticRegression
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA

lda = LDA(n_components=2)
lr = LogisticRegression()
X_train_lda = lda.fit_transform(X_train_std, y_train)
X_test_lda = lda.transform(X_test_std)
lr.fit(X_train_lda, y_train)
plot_decision_regions(X_train_lda, y_train, classifier=lr)
plt.xlabel('LD 1')
plt.ylabel('LD 2')
plt.legend(loc='lower left')
plt.show()

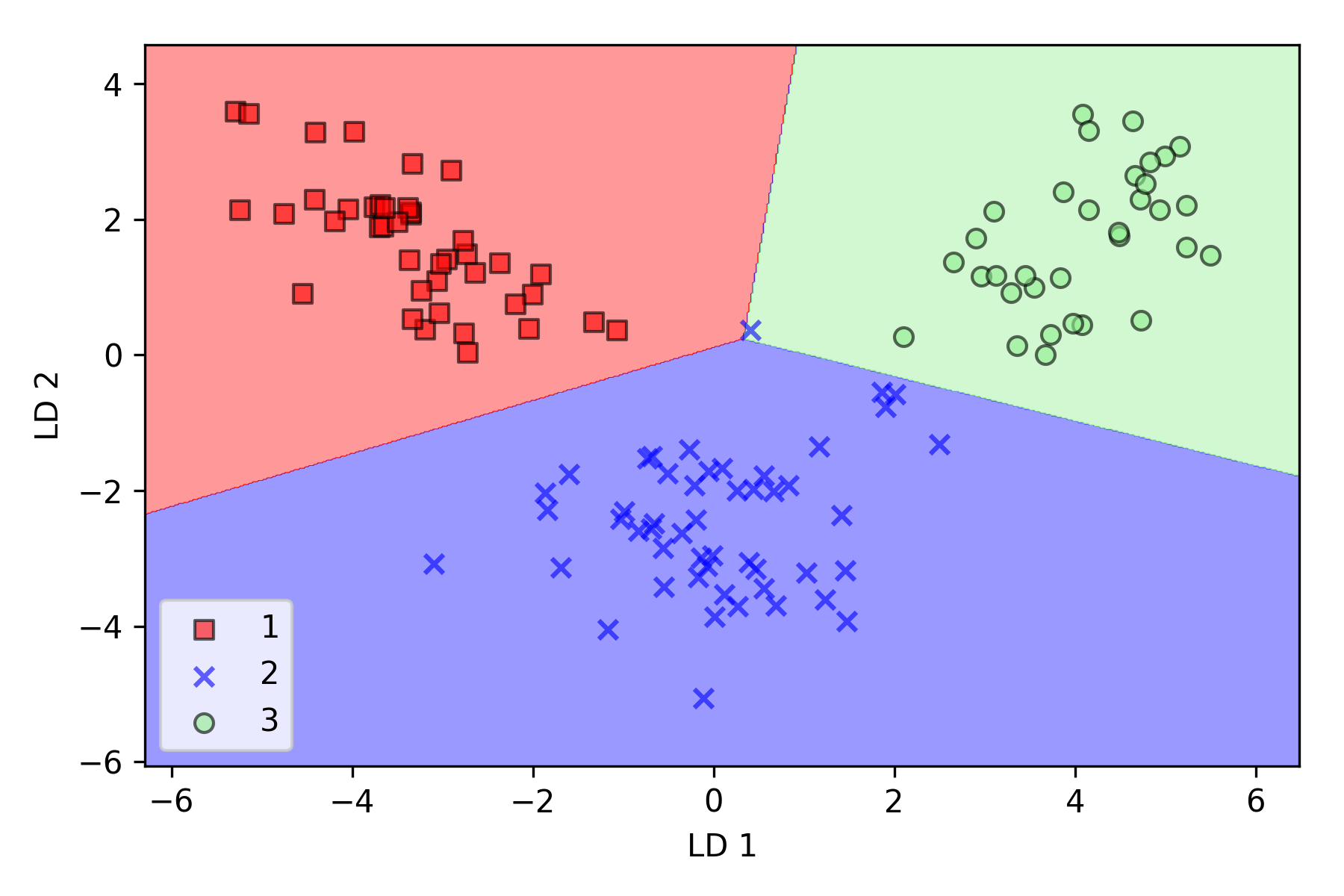
在降维空间绘制已通过训练得到的决策边界，观察是否能够进行很好地分类：

1
2
3
4
5
plot_decision_regions(X_test_lda, y_test, classifier=lr)
plt.xlabel('LD 1')
plt.ylabel('LD 2')
plt.legend(loc='lower left')
plt.show()

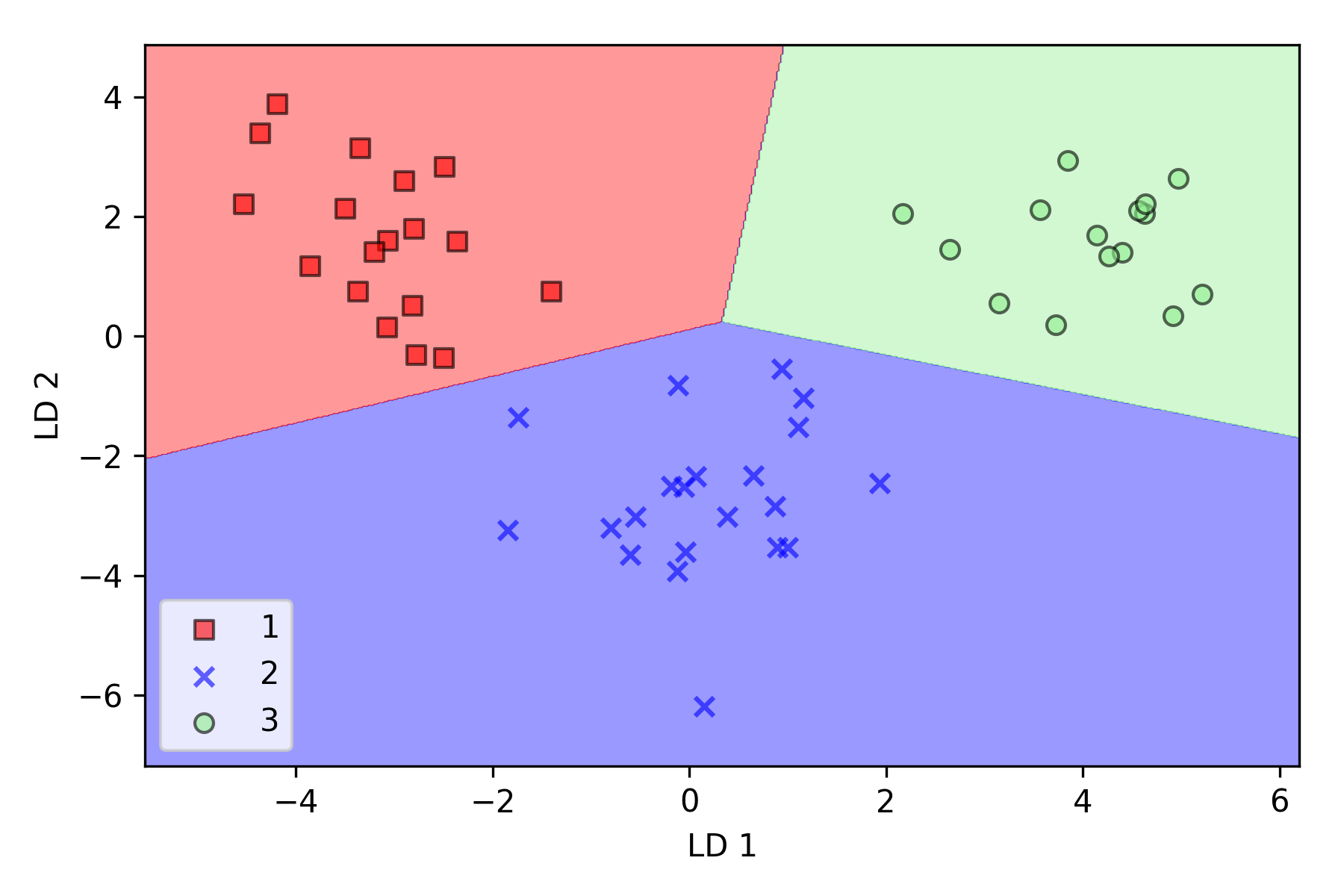
可以看到逻辑回归在新的二维子空间上表现很好，在测试数据集上只有很少样本分类错误。