主成分分析

与特征选择类似，我们可以使用特征提取（Feature Extraction）来减少数据集中特征的数量。其区别在于，特征选择保留原始特征，而特征提取则将数据转换或投影到新的特征空间。
本文介绍主成分分析（Principal Component Analysis, PCA），它是一种无监督的线性变换技术，主要特点是特征提取和降维。

算法思想

PCA 广泛应用于不同领域，帮助我们根据特征之间的相关性来识别数据中的模式。其原理是找到高维数据中最大方差的方向，并将其投影到与原始维数相同或更少维数的新的正交空间上。

新的子空间的正交轴（即主成分）可以被解释为在新的特征轴彼此正交的约束下的最大方差的方向，如下图所示：

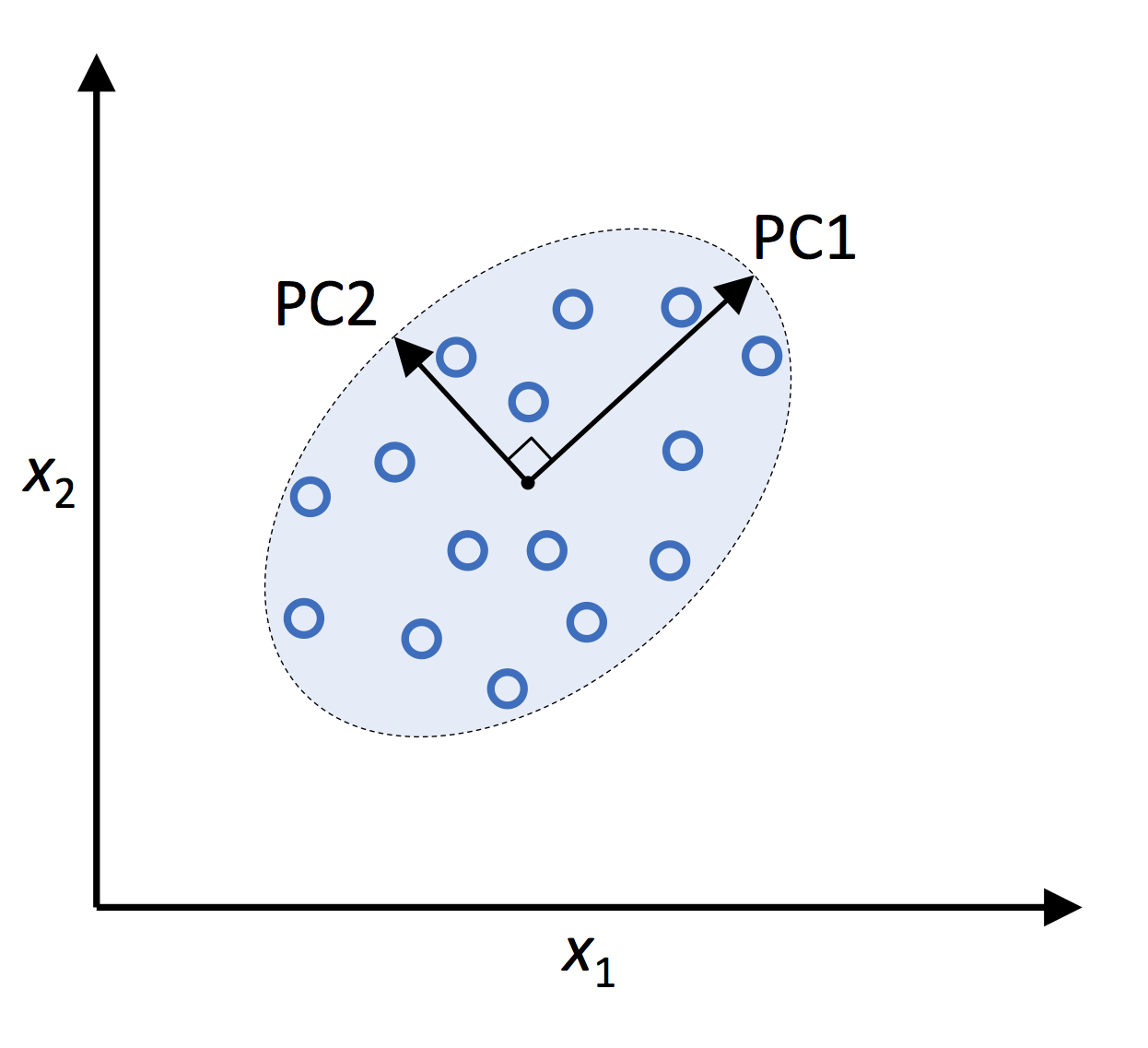
在上图中，$x_1$ 和 $x_2$ 是原始特征轴，PC1 和 PC2 是数据集的第一主成分和第二主成分。

PCA 构造了一个维度变换矩阵 $\boldsymbol W$，将高维空间向量 $\boldsymbol x$ 映射到低维空间向量 $\boldsymbol z$：

$$\begin{align} \boldsymbol x & = [x_1, x_2, \cdots, x_d], x \in R^d \\ & \downarrow \boldsymbol x \boldsymbol W, \boldsymbol W \in R^{d \times k} \\ \boldsymbol z & = [z_1, z_2, \cdots, z_k], z \in R^k \end{align}$$

维度变换后，第一主成分将具有最大的方差，第二主成分将具有第二大的方差，以此类推。这些主成分必须均不相关（即使输入特征之间有相关性），数学表示为主成分向量之间两两正交。

需要注意的是，PCA 方向对数据缩放非常敏感。举例来说，假设一个特征在 [-100,100] 之间平均分布，另外一个特征在 [-1,1] 之间平均分布，PCA 会认为前一个特征重要得多。因此在运用 PCA 时，需要使用标准化将输入特征缩放到相同的尺度。

PCA 的算法流程的简单介绍如下：

1. 对输入的 $d$ 维数据集 $\boldsymbol X$ 进行标准化。
2. 构造协方差矩阵。
3. 计算协方差矩阵的特征向量和特征值。
4. 对特征值进行降序排序，对相应的特征向量进行排序。
5. 提取 $k$ 个最大特征值对应的特征向量，其中 $k$ ($k \le d$) 是新特征子空间的维数。
6. 使用提取的 $k$ 个特征向量构造投影矩阵 $\boldsymbol W$。
7. 使用投影矩阵 $\boldsymbol W$ 对 $\boldsymbol X$ 进行变换，得到新的 $k$ 维特征子空间。

数据导入和标准化

导入 Wine 数据集 ，第 1 列为其分类标签，第 2~14 列为特征。分割数据集为 70% 的训练集和 30% 的测试集：

import pandas as pd
from sklearn.model_selection import train_test_split

df_wine = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data', header=None)
X, y = df_wine.iloc[:, 1:].values, df_wine.iloc[:, 0].values
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0, stratify=y)

对训练集和测试集进行标准化：

from sklearn.preprocessing import StandardScaler

sc = StandardScaler()
sc.fit(X_train)
X_train_std = sc.transform(X_train)
X_test_std = sc.transform(X_test)

协方差矩阵的构造

接下来引入协方差矩阵。对于 $n$ 的两个特征向量（机器学习中通常用列向量表示） $\boldsymbol x_j$ 和 $\boldsymbol x_k$，其协方差如下：

$$\begin{align} \sigma_{jk} = \sigma_{kj} = {\frac 1 n} \sum_{i=1}^n (x_j^{(i)} - \mu_j)(x_k^{(i)} - \mu_k) \end{align}$$

其中 $\mu_j$ 和 $\mu_k$ 分别代表 $\boldsymbol x_j$ 和 $\boldsymbol x_k$ 平均值。对于 PCA 的样本，在标准化后这两个平均值都为 0 。

协方差 $\sigma_{jk}$ 可以表示 $\boldsymbol x_j$ 和 $\boldsymbol x_k$ 的相关程度：

• 若 $\sigma_{jk}$ 大于 0，表明这两个特征正相关，即一个特征随另外一个特征的变大而变大。
• 若 $\sigma_{jk}$ 大于 0，表明这两个特征负相关，即一个特征随另外一个特征的变大而变小。
• 若 $\sigma_{jk}$ 等于 0，表明这两个特征不相关，即一个特征变化不受另外一个特征的变化影响。此时这两个特征向量两两正交。

接下来构建协方差矩阵 $\boldsymbol \Sigma$（这是大写的希腊字母 Sigma，不要与求和符号 $\sum$ 混淆）。以 3 个特征为例，其协方差矩阵如下：

$$\begin{align} \boldsymbol \Sigma = \begin{bmatrix} \sigma_1^2 & \sigma_{12} & \sigma_{13} \\ \sigma_{21} & \sigma_2^2 & \sigma_{23} \\ \sigma_{31} & \sigma_{32} & \sigma_3^2 \end{bmatrix} \end{align}$$

协方差矩阵 $\boldsymbol \Sigma$ 是实对称矩阵，矩阵对角线为特征的方差，其余为特征之间的协方差。$\boldsymbol \Sigma$ 的特征向量表示主成分（即具有最大方差的方向），对应的特征值为主成分的大小。

Wine 数据集有 13 个特征，我们将从 13×13 维协方差矩阵中获得 13 个特征向量和特征值。

特征值和特征向量

求解矩阵的特征值 $\lambda$ 和特征向量 $\boldsymbol v$，使其满足条件：

$$\begin{align} {\boldsymbol \Sigma} {\boldsymbol v} = \lambda {\boldsymbol v} \end{align}$$

矩阵特征值和特征向量的数学计算较为繁琐，这里不作过多介绍。

使用 numpy 内置的 linalg.eig 函数可以方便地计算特征值和特征向量：

import numpy as np

cov_mat = np.cov(X_train_std.T)
eigen_vals, eigen_vecs = np.linalg.eig(cov_mat)

上面通过 numpy.cov 创建协方差矩阵，然后通过 numpy.linalg.eig 对其进行特征分解，产生由 13 个特征值组成的向量 eigen_vals 和 13 个特征向量（列向量）组成的矩阵 eigen_vecs。

解释方差占比

把 $d$ 维空间压缩到 $k$ 维空间，需要从中挑选包含信息最多（方差最大）的 $k$ 个特征向量（主成分）。特征值反映了特征向量的大小，需要降序排序特征值，然后提取前 $k$ 个特征值对应的特征向量。

在提取特征之前，为了观察特征的方差之间的差异，这里先对特征值的解释方差占比（explained variance ratio）进行绘图：

import matplotlib.pyplot as plt

tot = sum(eigen_vals)
var_exp = [(i / tot) for i in sorted(eigen_vals, reverse=True)]
cum_var_exp = np.cumsum(var_exp)

plt.bar(range(1, 14), var_exp, alpha=0.5, align='center', label='individual explained variance')
plt.step(range(1, 14), cum_var_exp, where='mid', label='cumulative explained variance')
plt.ylabel('Explained variance ratio')
plt.xlabel('Principal component index')
plt.legend(loc='best')
plt.show()

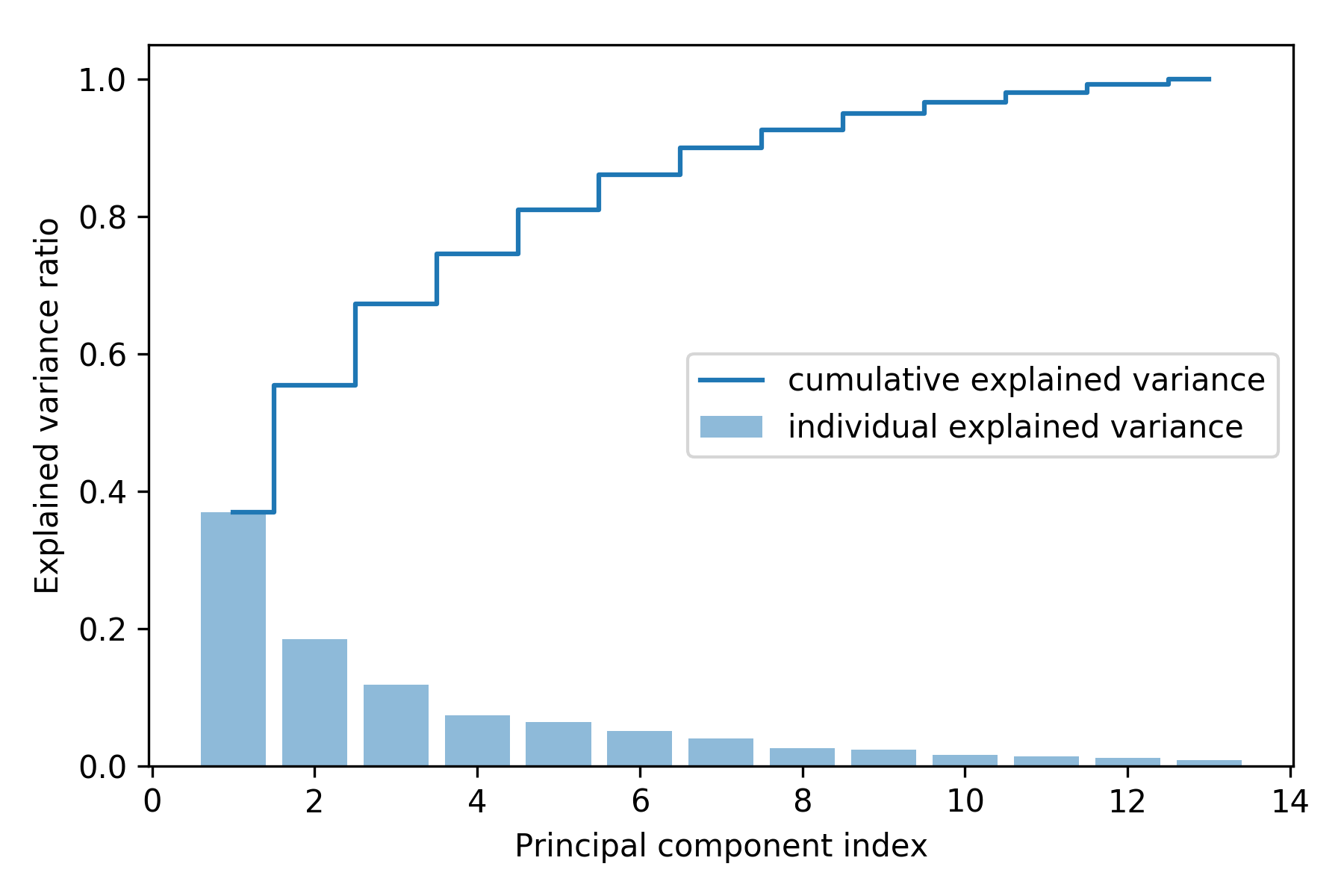
可以看到，第一主成分大约占了方差的 40%，第二主成分大约占了总方差的 20%，这两个特征值解释了接近 60% 的数据集方差。

需要注意的是，整个过程中没有使用 y_train。PCA 属于无监督学习，在分析和提取主成分的过程中从来不使用类的标签。

特征提取

本节以 Wine 数据集进行演示特征提取的最后几个步骤：

• 提取 $k$ 个最大特征值对应的特征向量，其中 $k$ ($k \le d$) 是新特征子空间的维数。
• 使用提取的 $k$ 个特征向量构造投影矩阵 $\boldsymbol W$，
• 使用投影矩阵 $\boldsymbol W$ 对 $\boldsymbol X$ 进行变换，得到新的 $k$ 维特征子空间。

简单来说，就是按照特征值降序将特征向量进行排序，从特征向量中构造投影矩阵，并使用投影矩阵将数据转换到低维子空间。

特征向量排序：

# Make a list of (eigenvalue, eigenvector) tuples
eigen_pairs = [(np.abs(eigen_vals[i]), eigen_vecs[:, i]) for i in range(len(eigen_vals))]
# Sort the (eigenvalue, eigenvector) tuples from high to low
eigen_pairs.sort(key=lambda k: k[0], reverse=True)

以两个主成分为例，构造投影矩阵：

注意，为了后面的绘制二维散点图，因此这里只挑选了两个主成分。实际中应该根据效率性能的平衡来确定主成分的个数。

w = np.hstack((eigen_pairs[0][1][:, np.newaxis], eigen_pairs[1][1][:, np.newaxis]))

使用投影矩阵转换原始数据集：

$$\begin{align} \boldsymbol x' & = \boldsymbol x \boldsymbol W \\ & \downarrow \\ \boldsymbol X' & = \boldsymbol X \boldsymbol W \end{align}$$

其中 $\boldsymbol X$ 为原始数据集，$\boldsymbol x$ 为其中的单个样本；$\boldsymbol X’$ 为变换后的数据集， $\boldsymbol x’$ 为其中的单个样本。

X_train_pca = X_train_std.dot(w)

原始的 Wine 数据集有 13 维，通过特征矩阵 $\boldsymbol W \in R^{13 \times 2}$ 后降为 2 维，对降维后的数据集进行绘图：

colors = ['r', 'b', 'g']
markers = ['s', 'x', 'o']
for l, c, m in zip(np.unique(y_train), colors, markers):
    plt.scatter(X_train_pca[y_train == l, 0], X_train_pca[y_train == l, 1], c=c, label=l, marker=m)
plt.xlabel('PC 1')
plt.ylabel('PC 2')
plt.legend(loc='lower left')
plt.show()

从下图可以看到，数据沿着 $x$ 轴（第一主成分）比沿着 $y$ 轴（第二主成分）更加分散，与上节中第一主成分的方差较大相吻合。另外，降维后的分类数据仍保留其特征，可以用线性分类器进行分类。

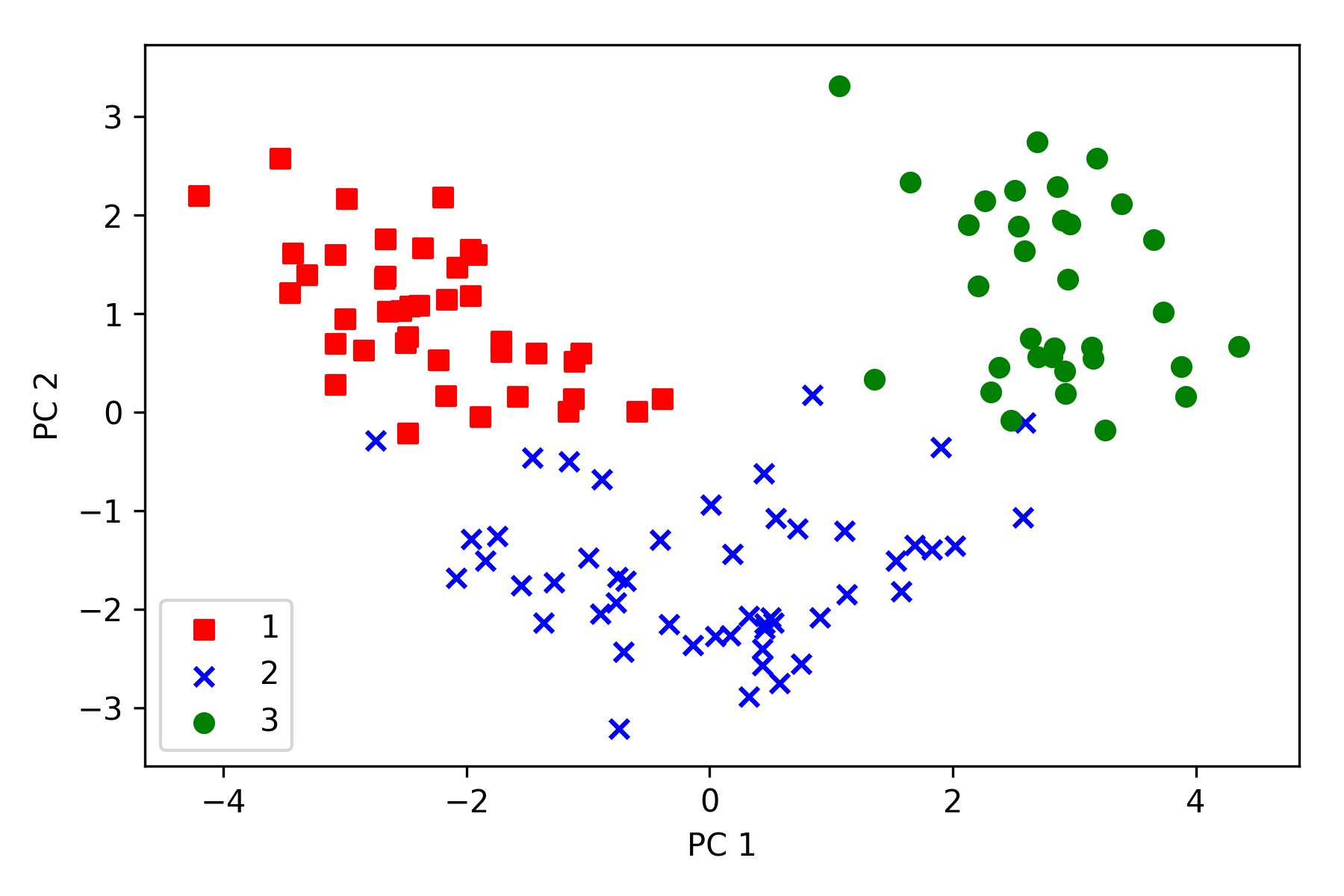
需要再次强调，PCA 是一种无监督的技术，在整个 PCA 过程中不使用任何类标签信息。

Scikit-learn 实现

边界绘图函数 plot_decision_regions 见之前的文章。

通过 sklearn.decomposition.PCA 将测试集和训练集降至二维，然后使用逻辑回归对降维后的测试集进行线性分类：

from sklearn.linear_model import LogisticRegression
from sklearn.decomposition import PCA

pca = PCA(n_components=2)
lr = LogisticRegression()
X_train_pca = pca.fit_transform(X_train_std)
X_test_pca = pca.transform(X_test_std)
lr.fit(X_train_pca, y_train)
plot_decision_regions(X_train_pca, y_train, classifier=lr)
plt.xlabel('PC 1')
plt.ylabel('PC 2')
plt.legend(loc='lower left')
plt.show()

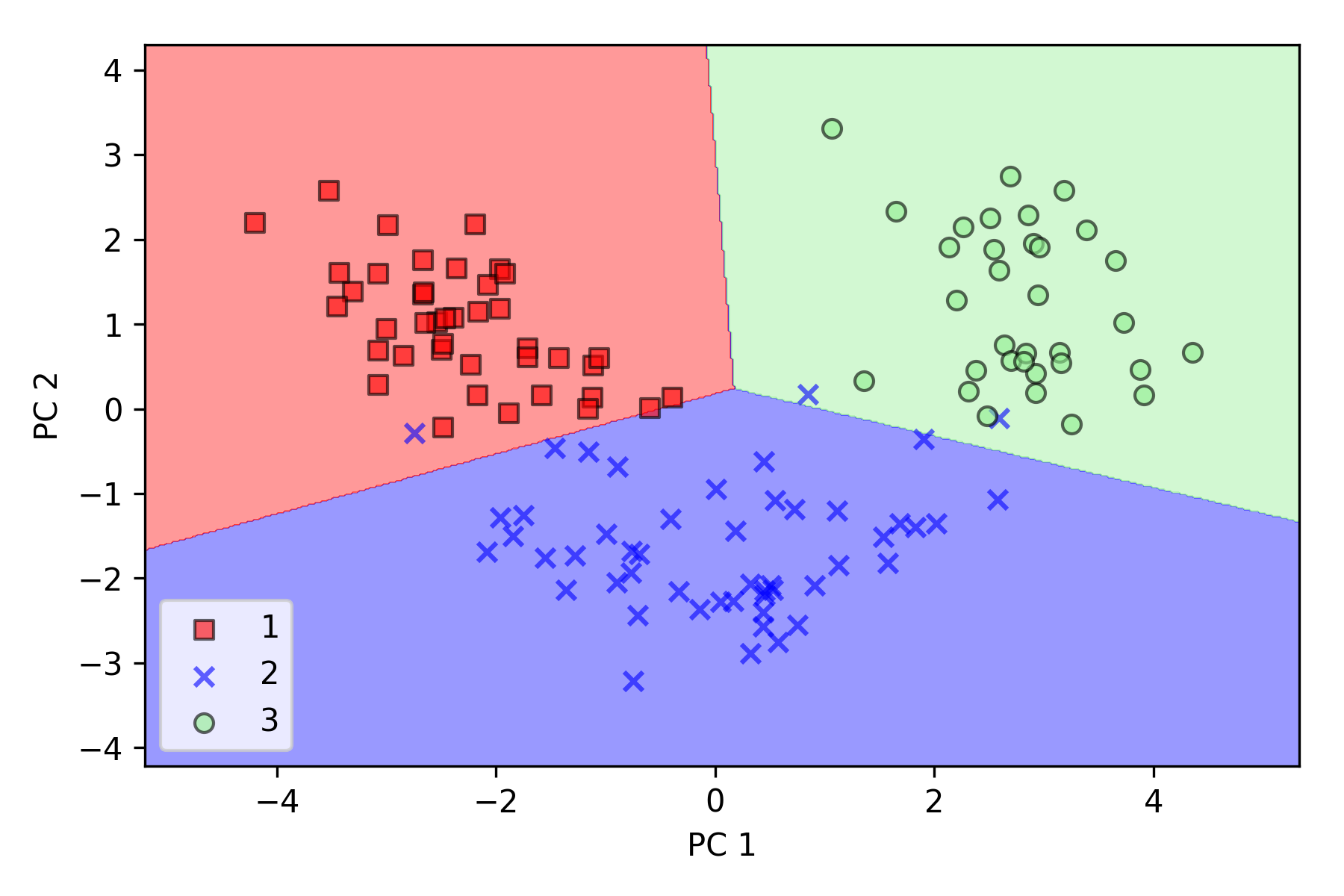
在降维空间绘制已通过训练得到的决策边界，观察是否能够进行很好地分类：

plot_decision_regions(X_test_pca, y_test, classifier=lr)
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.legend(loc='lower left')
plt.show()

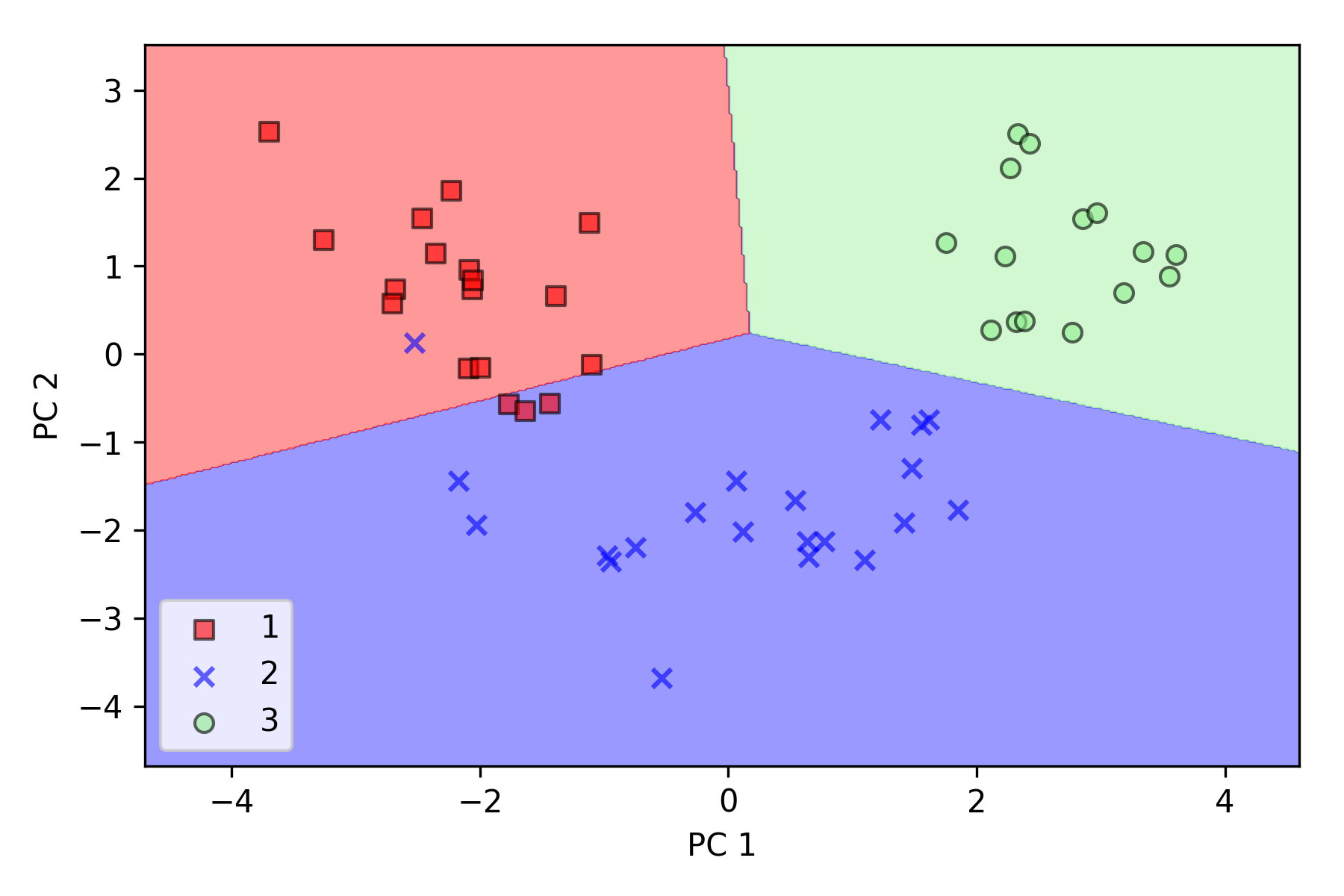
可以看到逻辑回归在新的二维子空间上表现很好，在测试数据集上只有很少样本分类错误。

关于数据集的解释方差占比，可以设置 PCA 的参数 n_components 为 None，对测试集进行变换后通过 explained_variance_ratio_ 属性得到：

pca = PCA(n_components=None)
X_train_pca = pca.fit_transform(X_train_std)
print(pca.explained_variance_ratio_)