TensorFlow 官方教程：面向初学者的 MNIST

发表于 | 分类于

本教程基于 TensorFlow - MNIST For ML Beginners ，其中有一些基于个人理解的删减和添加。

2018 年 2 月 1 日 更新：官方移除了这份入门教程，并将原链接重定向至 A Guide to TF Layers 。

MNIST 数据集

MNIST 简介

MNIST 是一个简单的计算机视觉数据集，由手写数字（0~9）的图像组成，如下：

它还包括每个图像的标签，上述图像的标签是 5，0，4 和 1。

本教程将训练一个模型，用来预测图案代表的数字。

通过下面两行代码导入 MNIST 数据集：

1
2
3
from tensorflow.examples.tutorials.mnist import input_data

mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)

MNIST 数据分为三个部分：55,000 个样本（mnist.train）的训练数据集，10,000 个样本（mnist.test）的测试数据集，以及 5,000 个样本（mnist.validation）的验证数据集。

每个 MNIST 数据有两部分：手写数字的图像 x，以及对应的标签（即图像实际代表的数字）y。例如测试集图像为 mnist.train.images，测试集标签为 mnist.train.labels。

其中每个手写的图像为 28 × 28 像素，每个像素代表灰度（黑色为 1，白色为 0，灰色介于两者之间），如下示意图：

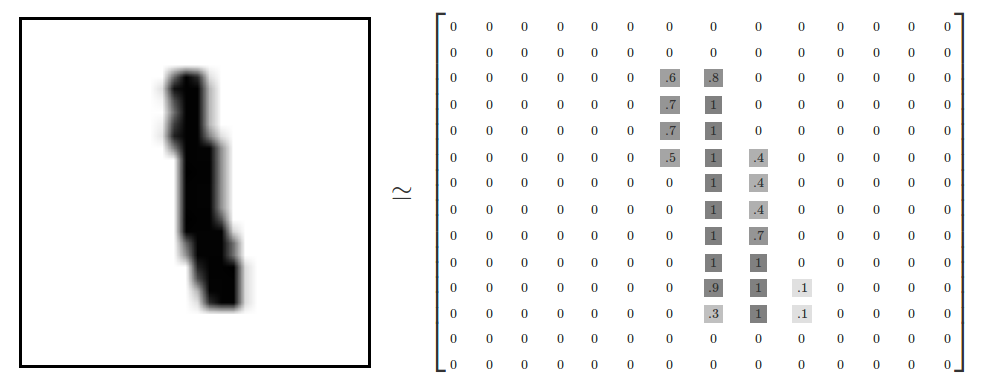
MNIST 数据展开

每张图像有 784 个像素，可以将 MNIST 图像可以转换为 28x28 = 784 维向量空间中的某一点，其中每个维度的点为对应的灰度。

展开数据会丢弃有关图像二维结构的信息，但本文为采用 softmax 的入门教程，故不对此作讨论。

将 mnist.train.images 转换为形状为 [55000, 784] 的张量。第一维代表图像列表的索引，第二维代表像素列表的索引。张量中的每个数值代表灰度。

MNIST 中的每个图像都有相应的标签，即 0~9 中的某个数字。标签可以编码为独热向量（One-hot Vectors），对应维度的数字为 1，其余维度置 0。如标签 3 可以编码为 [0,0,0,1,0,0,0,0,0,0]。

将 mnist.train.images 转换为形状为 [55000, 10] 的张量。第一维代表图像列表的索引，第二维代表独热向量。

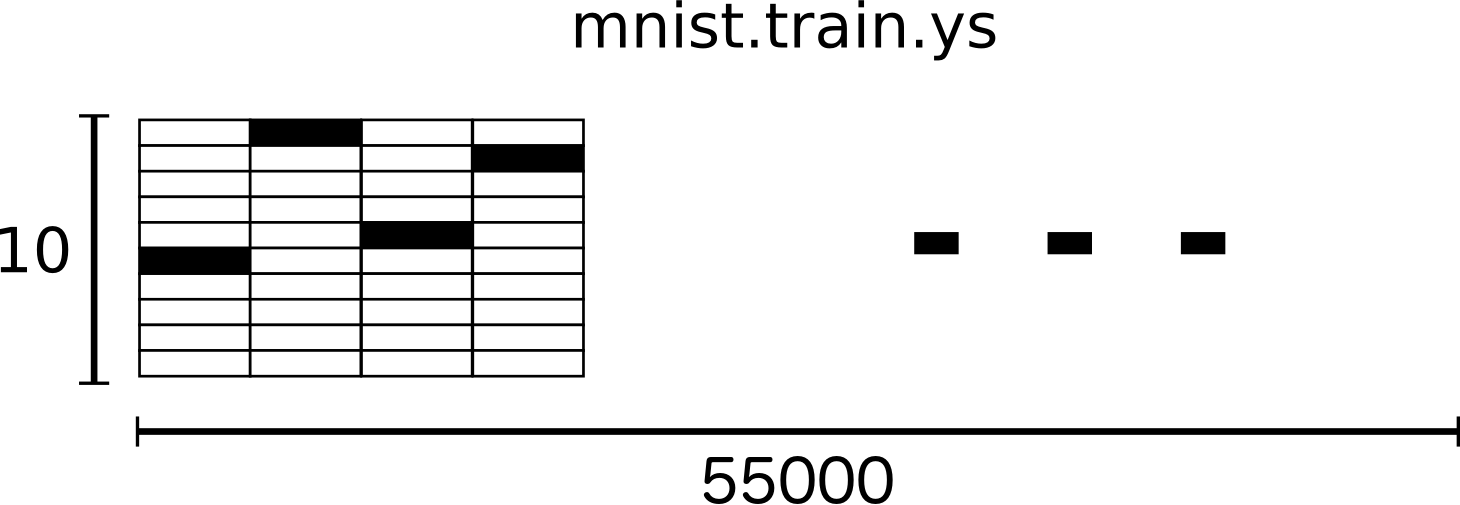
Softmax 回归

本节对 softmax 回归介绍较为简略，更多信息请自行搜索相关文档。

MNIST 中的每张图像，只有十个可能输出。这里用到 softmax 回归，输出对应的概率。

例如对于某张图片，我们希望模型有 80% 预测是 “9”，有 5% 的概率是 “8”（因为 8 和 9 上部分有点相似），预测为其他数字的概率为 15%。

softmax 回归可以解决这个问题，输出对应每个类别的概率。

在介绍 softmax 回归之前，先介绍一下 softmax。其思想是先对输入的数值列表进行指数化（映射为正数），然后进行标准化（转换为概率）。

$$\begin{align} \text{softmax}(evidence)_i = \frac{\exp(evidence_i)}{\sum_j \exp(evidence_j)} \end{align}$$

softmax 回归如下图所示，其中 x 为输出，W 为权重，b 为偏差，然后对于每个输出计算 softmax：

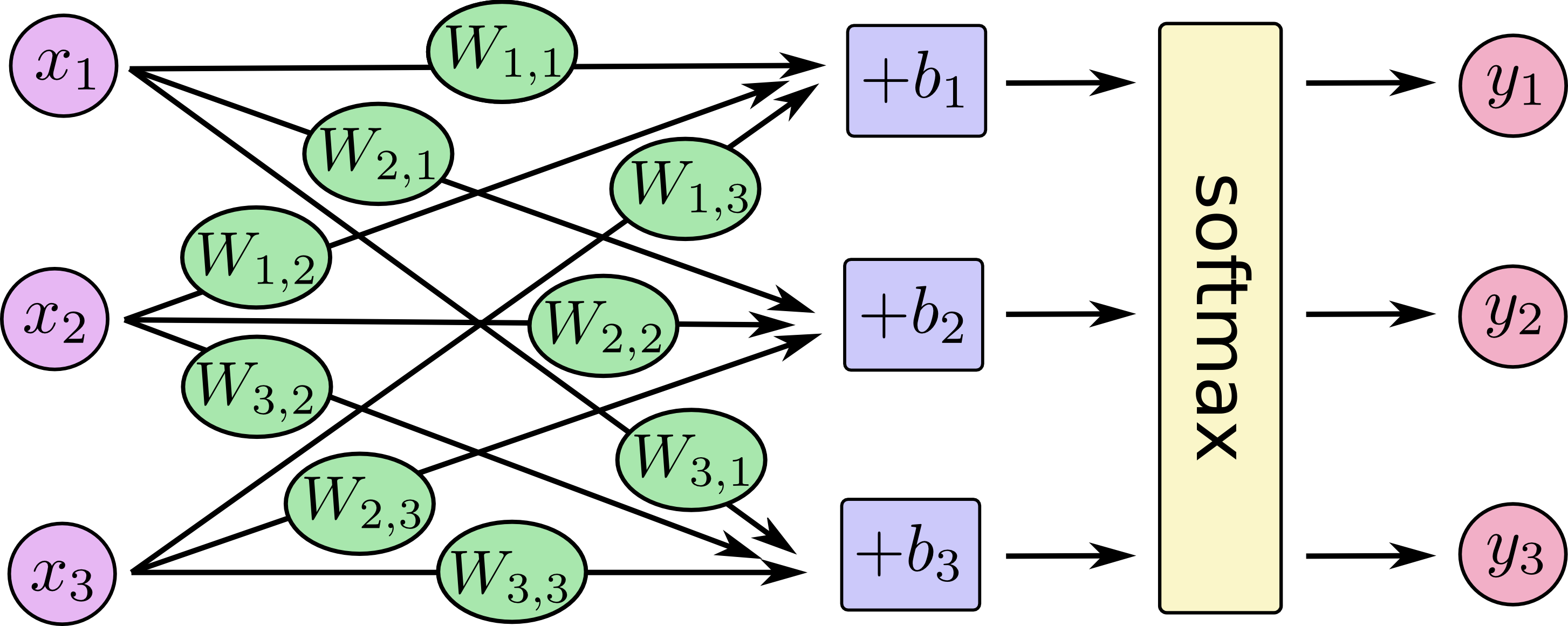
向量化表示为：

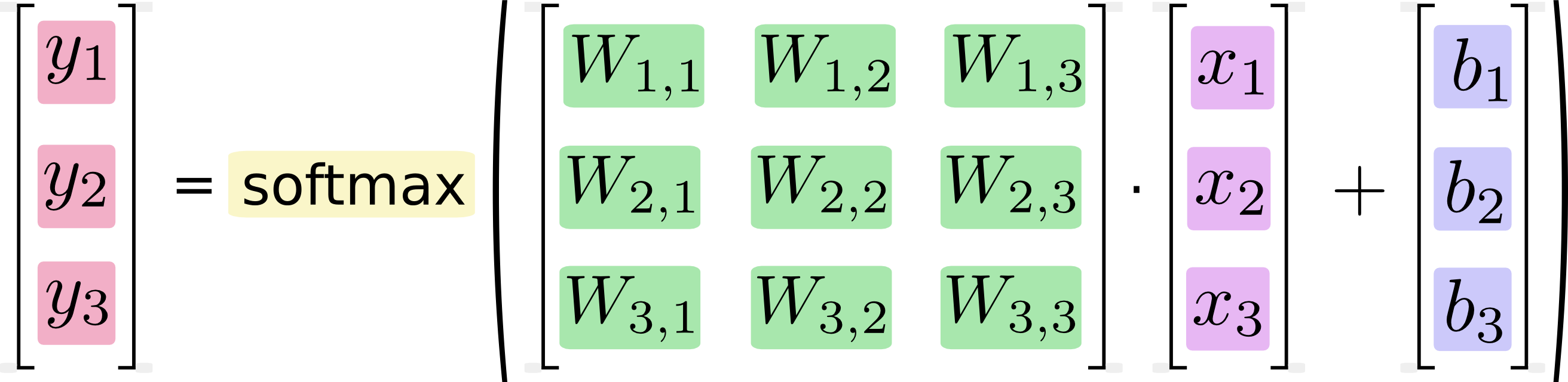
即：

$$\begin{align} y = \text{softmax}(Wx + b) \end{align}$$

TensorFlow 实现

模型定义

导入 TensorFlow 库：

1
import tensorflow as tf

定义输入 x 为形状 [None, 784] 的 2 维张量：

1
x = tf.placeholder(tf.float32, [None, 784])

定义输入 x 为形状 [None, 784] 的 2 维张量

None 代表可以为任意数据。按照惯例，代表样本数量的位置需要定义为 None。

定义权重张量 W 和偏差张量 b，初始化其中的值为 0：

1
2
W = tf.Variable(tf.zeros([784, 10]))
b = tf.Variable(tf.zeros([10]))

计算模型的加权输出 y，这里暂时不使用 softmax 回归，后文会说明：

1
y = tf.matmul(x, W) + b

定义正确标签 y_ 为形状 [None, 10] 的 2 维张量：

1
y_ = tf.placeholder(tf.float32, [None, 10])

模型训练

计算正确标签 y_ 和模型加权输出 y 之间的 softmax 交叉熵（请参见附注：softmax 交叉熵的计算）：

1
cross_entropy = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y_, logits=y))

定义训练操作，在每次训练中使用学习率为 0.5 的梯度下降法优化器，对交叉熵进行最小化：

1
train_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)

在这里，TensorFlow 实际上在图中添加了一些操作，以实现反向传播和梯度下降。运行 train_step 时，图中进行单次梯度下降，对变量 W 和 b 进行调整，以降低交叉熵。

导入 TensorFlow 的交互式会话：

1
sess = tf.InteractiveSession()

初始化变量：

1
tf.global_variables_initializer().run()

进行 1000 次小批量（Mini-Batch）梯度下降训练，每个小批量包含测试集中的 100 个样本：

1
2
3
for _ in range(1000):
  batch_xs, batch_ys = mnist.train.next_batch(100)
  sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})

模型评估

tf.argmax 可以计算某个轴上张量的最大项的索引。tf.argmax(y,1) 代表最高概率的预测标签，而 tf.argmax(y_,1) 代表正确的标签。

1
correct_prediction = tf.equal(tf.argmax(y,1), tf.argmax(y_,1))

上述得到含有布尔值的列表。预测的准确率如下：

1
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

例如，[True, False, True, True] 代表为 3 个样本预测正确，1 个样本预测错误。通过上式转换得到的 accuracy 为 0.75。

最后一步，计算模型在测试集上的准确率：

1
print(sess.run(accuracy, feed_dict={x: mnist.test.images, y_: mnist.test.labels}))

上述输出大概为 0.92。这个结果差强人意，因为本文采用的是最简单的模型。若采用复杂些的模型，可以将模型的准确率提高到 97% 甚至更高。

附注：softmax 交叉熵的计算

softmax 交叉熵的计算，建议如正文中使用函数 tf.nn.softmax_cross_entropy_with_logits，把未经 softmax 的加权输出直接传到此函数的 logits 参数。

按照原始公式的实现如下（分开计算 softmax 和交叉熵），但不推荐。按照官方说明，这种实现可能会导致输出值不稳定。

1
2
y = tf.nn.softmax(y)
cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y), reduction_indices=[1]))