逻辑回归

发表于 | 分类于

逻辑回归（Logistic Regression）是一种非常容易实现的分类模型，对于线性可分的情况有很好的表现。
与之前文章中的感知器和 Adaline 类似，本文中的逻辑回归也是二元分类的线性模型。

算法思想

为了解释逻辑回归模型背后的思想，先介绍一个概念：比值比（Odds ratio, OR）。

比值比的数学表示为 $\cfrac p {1-p}$，其中 $p$ 为某事件可能发生的几率。

在此基础上，定义 logit 函数，即比值比的对数（计算机科学中 $\log$ 表示自然对数）：

$$\begin{align} logit(p) = \log {\cfrac p {1-p}} \end{align}$$

logit 的作用是将范围为 $(0,1)$ 的变量，映射到整个实数集。

对于给定的 $x$：

  • $y=1$ 的概率 $p(y=1\ | x)$ 在 $(0,1)$ 之间。
  • 基于神经元模型，输出的概率是由净输入 $z = \sum_{i=0}^m w_i x_i = w^T x$ 得到的。

基于以上逻辑，建立 $p(y=1\ \mid x) \rightarrow z$ 的 logit 映射：

$$\begin{align} logit(p(y=1 \mid x)) = z \end{align}$$

因此，logit 的反函数即为 $z \rightarrow p(y=1\ \mid x)$ 的映射：

$$\begin{align} \phi (z) = \cfrac 1 {1+e^{-z}} = p(y=1 \mid x) \end{align}$$

这里 $\phi (z) = \cfrac 1 {1+e^{-z}}$ 称为 logistic sigmoid 函数，通常简称为 sigmoid 函数。（sigmoid 意为 S-shaped，即 S 形状的曲线。）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
import matplotlib.pyplot as plt
import numpy as np


def sigmoid(z):
    return 1.0 / (1.0 + np.exp(-z))


z = np.arange(-7, 7, 0.1)
phi_z = sigmoid(z)

plt.plot(z, phi_z)
plt.axvline(0.0, color='k')
plt.ylim(-0.1, 1.1)
plt.xlabel('z')
plt.ylabel('$\phi (z)$')
plt.yticks([0.0, 0.5, 1.0])
ax = plt.gca()
ax.yaxis.grid(True)
plt.show()

算法模型

Adaline 和 逻辑回归的差异，如下图所示：

Adaline：

  • 激活函数：线性函数 $\phi (z) = z$
  • 阈值函数：阶跃函数 $\hat y = \begin{cases} 1 & if \ \phi (z) \ge 0 \\[2ex] 0 & otherwise \end{cases}$

逻辑回归：

  • 激活函数：sigmoid 函数 $\phi (z) = \cfrac 1 {1+e^{-z}}$
  • 阈值函数：阶跃函数 $\hat y = \begin{cases} 1 & if \ \phi (z) \ge 0.5 \\[2ex] 0 & otherwise \end{cases}$

需要注意的是，逻辑回归中的条件 $\phi (z) \ge 0.5$，等价于 $z \ge 0$。

损失函数和成本函数

定义损失函数（Loss Fucntion）和成本函数（Cost Fucntion），以训练权重参数 $w$。

损失函数用于单个样本，代表预测输出 $\hat y^{(i)}$ 和实际输出 $y^{(i)}$ 之间的误差。

$$\begin{align} L(\hat y^{(i)}, y^{(i)}) & = -[y^{(i)} \log (\hat y^{(i)}) + (1 - y^{(i)}) \log (1 - \hat y^{(i)})] \\ & = \begin{cases} -\log (\hat y^{(i)}) & \text{if} \ y^{(i)} = 1 \\[2ex] -\log (1 - \hat y^{(i)}) & \text{if} \ y^{(i)} = 0\end{cases} \end{align}$$
  • 当 $y^{(i)} = 1$ 时，最小化 $L$ 等价于 $\hat y^{(i)}$ 接近于 1。
  • 当 $y^{(i)} = 0$ 时，最小化 $L$ 等价于 $\hat y^{(i)}$ 接近于 0。

成本函数是整个训练集的损失函数的平均值。最小化成本函数，可以得到最优的参数 $w$。

$$\begin{align} J(w) & = {\frac 1 m} \sum _{i=1}^m L(\hat y^{(i)}, y^{(i)}) \\ & = -{\frac 1 m} \sum _{i=1}^m [y^{(i)} \log (\hat y^{(i)}) + (1 - y^{(i)}) \log (1 - \hat y^{(i)})] \end{align}$$

Python 实现

逻辑回归的实现如下，使用梯度下降法进行参数训练：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
import numpy as np


class LogisticRegressionGD(object):
    def __init__(self, eta=0.05, n_iter=100, random_state=1):
        self.eta = eta
        self.n_iter = n_iter
        self.random_state = random_state

    def fit(self, X, y):
        rgen = np.random.RandomState(self.random_state)
        self.w_ = rgen.normal(loc=0.0, scale=0.01,
                              size=1 + X.shape[1])
        self.cost_ = []
        for i in range(self.n_iter):
            net_input = self.net_input(X)
            output = self.activation(net_input)
            errors = (y - output)
            self.w_[1:] += self.eta * X.T.dot(errors)
            self.w_[0] += self.eta * errors.sum()
        cost = -(y.dot(np.log(output)) + ((1 - y).dot(np.log(1 - output)))) / X.shape[0]
        self.cost_.append(cost)
        return self

    def net_input(self, X):
        return np.dot(X, self.w_[1:]) + self.w_[0]

    def activation(self, z):
        return 1. / (1. + np.exp(-np.clip(z, -250, 250)))

    def predict(self, X):
        return np.where(self.net_input(X) >= 0.0, 1, 0)

绘制图像

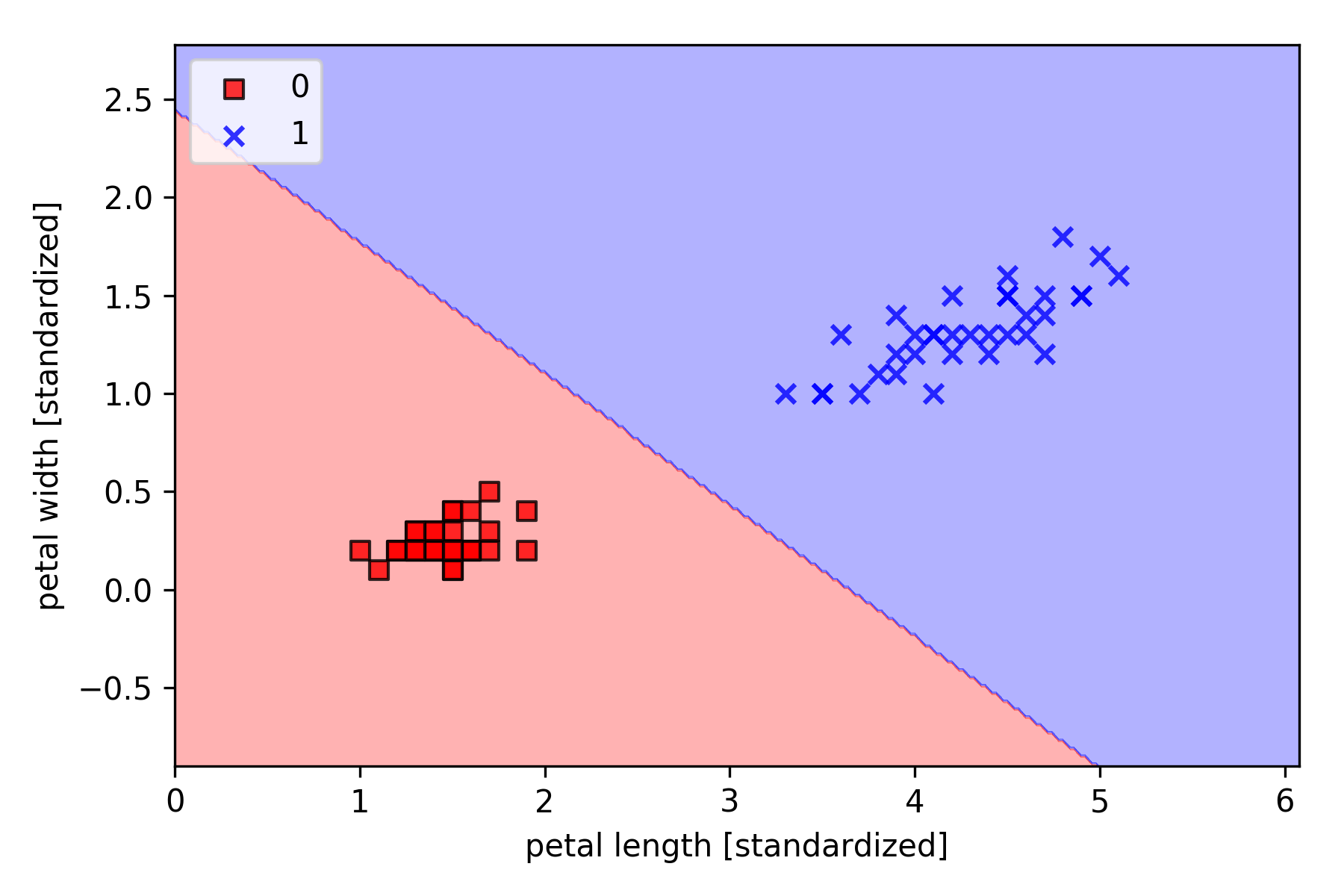
以 Iris-setosa（标签 0） and Iris-versicolor（标签 1）为例，采用逻辑回归分类，绘制决策边界如下，

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
import matplotlib.pyplot as plt
from plot_decision_regions import plot_decision_regions
from sklearn import datasets
from sklearn.model_selection import train_test_split

iris = datasets.load_iris()
X = iris.data[:, [2, 3]]
y = iris.target

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1, stratify=y)

X_train_01_subset = X_train[(y_train == 0) | (y_train == 1)]
y_train_01_subset = y_train[(y_train == 0) | (y_train == 1)]

lrgd = LogisticRegressionGD(eta=0.05,n_iter=1000,random_state=1)
lrgd.fit(X_train_01_subset,y_train_01_subset)

plot_decision_regions(X=X_train_01_subset,y=y_train_01_subset,classifier=lrgd)
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.legend(loc='upper left')
plt.show()