Adaline 和梯度下降法

发表于 | 分类于

本文介绍了基于梯度下降法（Gradient Descent，GD）的自适应线性神经元（Adaptive Linear Neuron，Adaline），以及对应的算法实现。

Adaline 原理

Adaline 是 1960 年由 Bernard Widrow 和 Tedd Hoff 提出的，被认为是对 Rosenblatt 感知器的改进。Adaline 算法定义了最小化成本函数的核心概念，为之后一些更先进的机器学习算法（如逻辑回归和支持向量机）奠定了基础。

Adaline 规则和 Rosenblatt 感知器的不同之处在于在调整权重的激活函数不同，前者采用线性函数，后者采用单位阶跃函数。
在 Adaline 中，$\phi(w^T x)= w^T x$。

Adaline 在使用线性激活函数更新权重之外，采用单位阶跃的量化器来预测类标签，如下图所示：

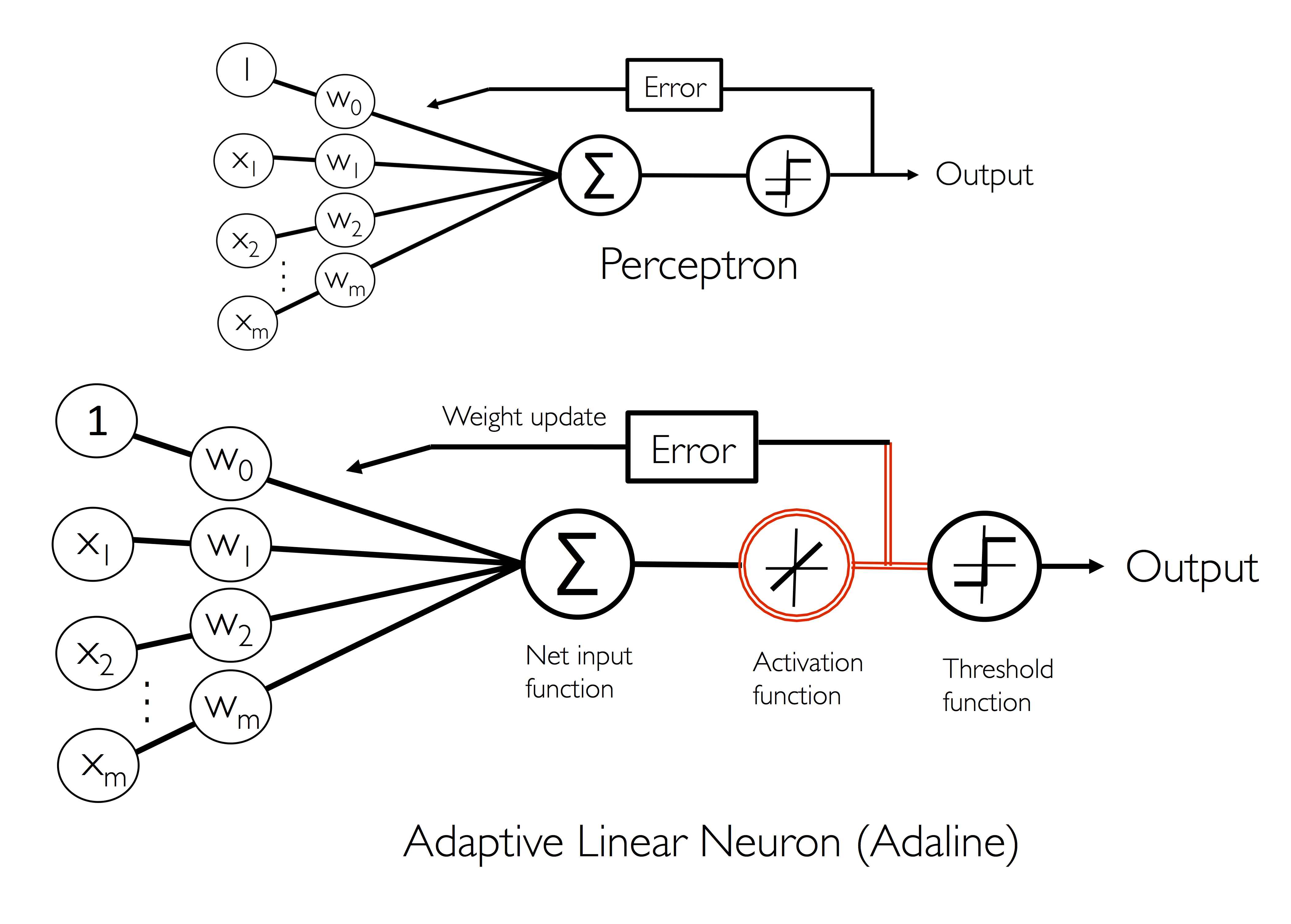
批量梯度下降法

定义在学习过程中需要优化的目标函数，是监督式学习的关键步骤。目标函数通常是需要最小化的成本函数。对于 Adaline，我们定义权重的成本函数 $J$ 为预测类标签和实际类标签之间的方差总和（Sum of Squared Errors，SSE）。

$$\begin{align} J(w) = {\frac 1 2} \Sigma_i(y^{(i)} - \phi(z^{(i)}))^2 \end{align}$$

线性激活函数的优点是，成本函数可微并且是凸函数（局部最小值为全局最小值）。

$$\begin{align} {\frac {\partial J(w)} {\partial w_j}} &= {\frac 1 2} {\frac {\Sigma_i(y^{(i)} - \phi(z^{(i)}))^2} {\partial z}} {\frac {\partial z} {\partial w_j}} \\ &= -{\Sigma_i(y^{(i)} - \phi(z^{(i)}))} x_j^{(i)} \end{align}$$

这里采用一种称为梯度下降的算法来找出最小化成本函数对应的权重，以便对 Iris 数据子集的样本进行分类。
如下图所示，可以将梯度下降类比成下山的过程，直到达到局部最小值。每次训练相当于在斜坡上行走一步，其中步长由学习率和斜率决定：

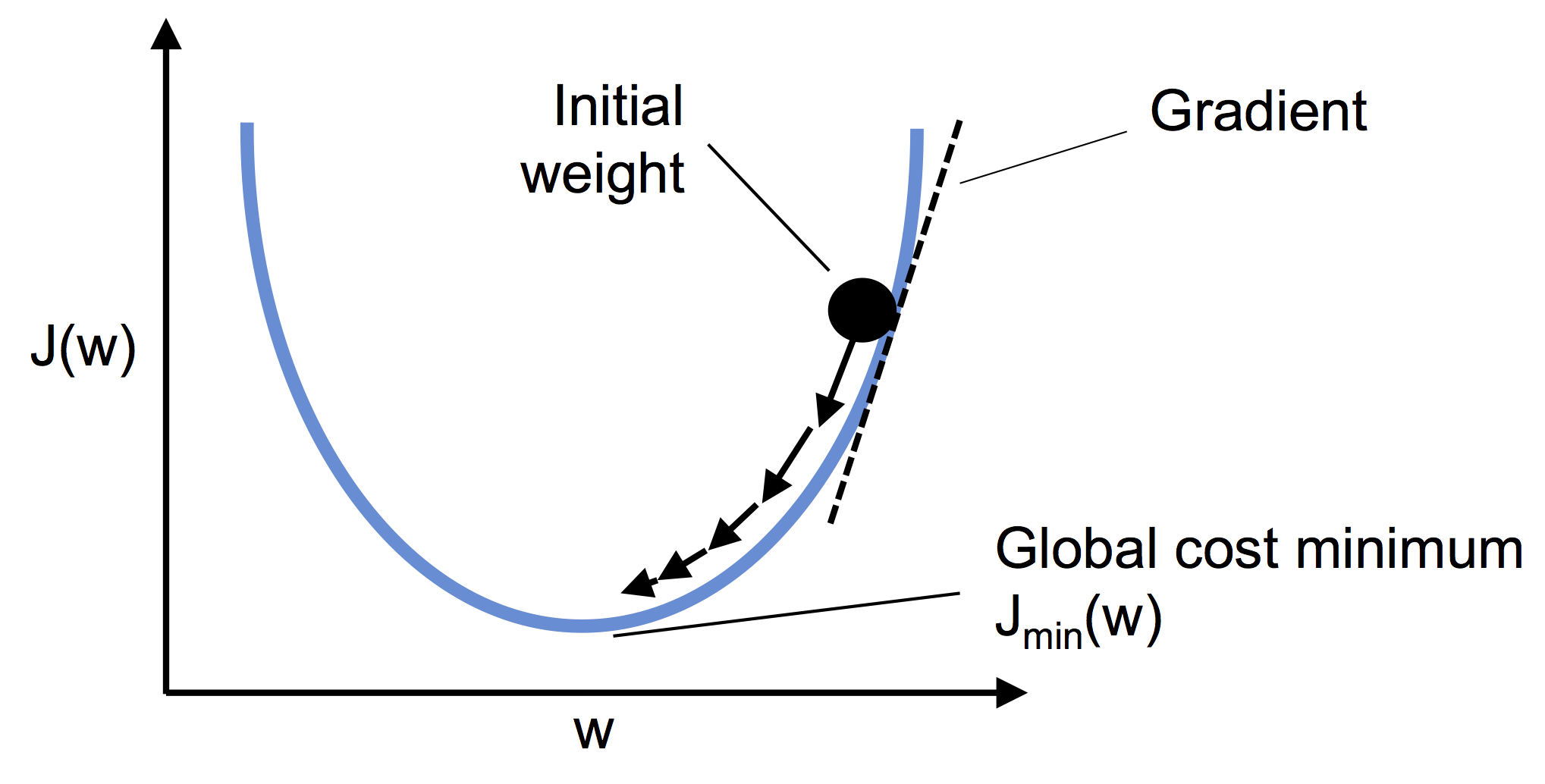
梯度下降法的思想是，如果函数在某点可微且有定义，那么函数在该点沿着梯度相反的方向下降最快，下降系数用学习率 $\eta$ 表示：

$$\begin{align} \Delta w_j = -\eta \Delta J(w) \end{align}$$

每次训练后，权重更新为：

$$\begin{align} w_j := w_j + \Delta w_j = w_j - \eta \Delta J(w) \end{align}$$

权重的每次更新是基于训练集中的所有样本（而并非单个样本），因此这种最原始的梯度下降法也被称为批量梯度下降法（Batch Gradient Descent，BGD）。

基于批量梯度下降法的 Adaline 实现

下面代码中，采用了面向对象的方法，定义 Adaline 为 Python 类。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
import numpy as np


class AdalineGD(object):
    def __init__(self, eta=0.01, n_iter=50, random_state=1):
        self.eta = eta
        self.n_iter = n_iter
        self.random_state = random_state

    def fit(self, X, y):
        rgen = np.random.RandomState(self.random_state)
        self.w_ = rgen.normal(loc=0.0, scale=0.01, size=1 + X.shape[1])
        self.cost_ = []

        for i in range(self.n_iter):
            net_input = self.net_input(X)
            output = self.activation(net_input)
            errors = y - output
            self.w_[1:] += self.eta * X.T.dot(errors)
            self.w_[0] += self.eta * errors.sum()
            cost = (errors ** 2).sum() / 2.0
            self.cost_.append(cost)
        return self

    def net_input(self, X):
        return np.dot(X, self.w_[1:]) + self.w_[0]

    def activation(self, X):
        return X

    def predict(self, X):
        return np.where(self.activation(X) >= 0.0, 1, -1)

对算法训练过程进行绘图：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
import pandas as pd
import matplotlib.pyplot as plt


df = pd.read_csv('https://archive.ics.uci.edu/ml/achine-learning-databases/iris/iris.data', header=None)
X = df.iloc[:100, [0, 2]].values
y = df.iloc[:100, 4].values
y = np.where(y == 'Iris-setosa', -1, 1)

fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(8, 4))

ada1 = AdalineGD(n_iter=10, eta=0.01).fit(X, y)
ax[0].plot(range(1, len(ada1.cost_) + 1), np.log10(ada1.cost_), marker='o')
ax[0].set_xlabel('Epochs')
ax[0].set_ylabel('log(Sum-squared-error)')
ax[0].set_title('Adaline - Learning rate 0.01')

ada2 = AdalineGD(n_iter=10, eta=0.0001).fit(X, y)
ax[1].plot(range(1, len(ada2.cost_) + 1), ada2.cost_, marker='o')
ax[1].set_xlabel('Epochs')
ax[1].set_ylabel('Sum-squared-error')
ax[1].set_title('Adaline - Learning rate 0.0001')

plt.tight_layout()
plt.show()

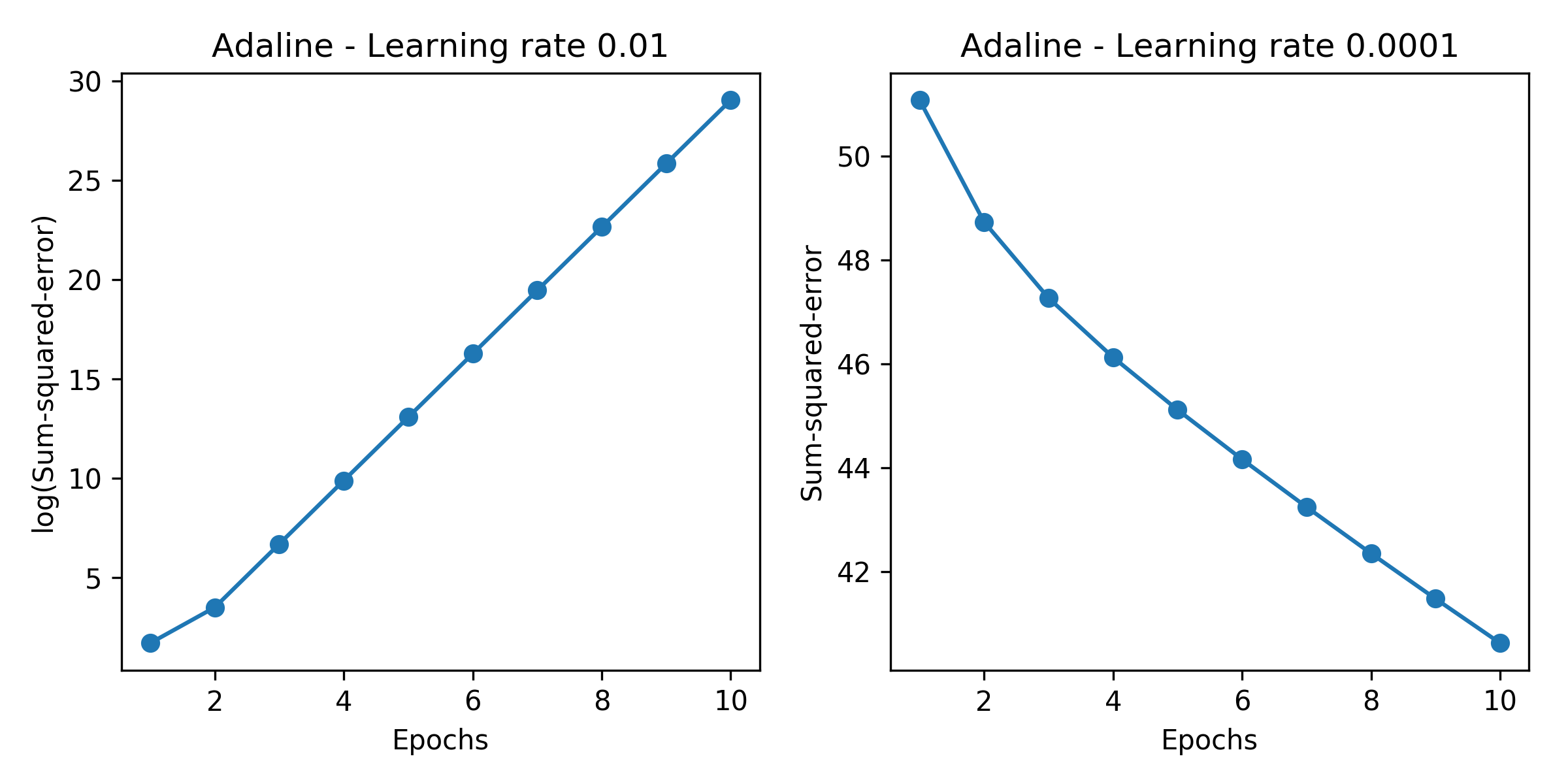
从上图中的左子图可以观察到，如果学习率太大，由于每次训练都越过了局部最小值，成本函数得不到最小化，反而错误会在学习过程中一直增加。右子图中，成本函数能够逐渐降低，但由于选择了非常小的学习率 $\eta = 0.0001$ ，以至于算法需要很长时间才能收敛。

下图中的左子图说明了成本函数随权重的调整而最小化，右子图说明了学习率太大所带来的问题：

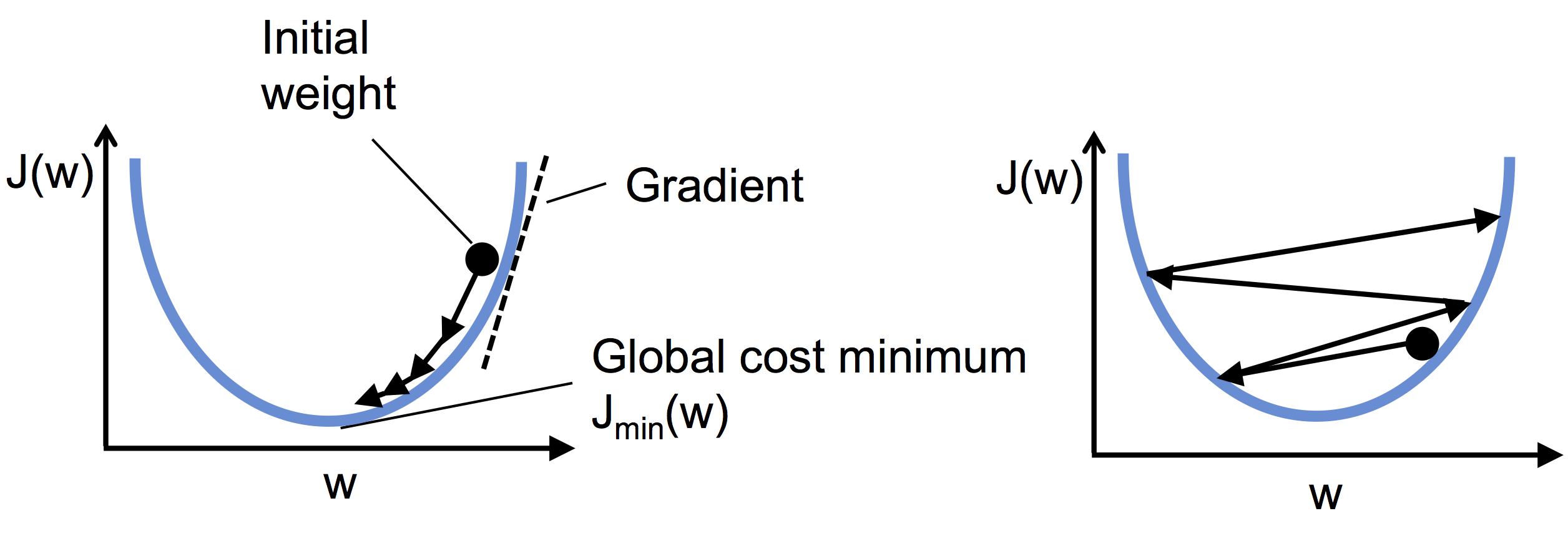
许多机器学习算法需要某些方法才能实现最佳性能，梯度下降法是从特征缩放（feature scaling）中受益的许多算法之一。这里我们将使用一种称为标准化（standardization）的特征缩放方法，能够将数据变换成服从标准正态分布（平均值为 0，标准差为 1）。

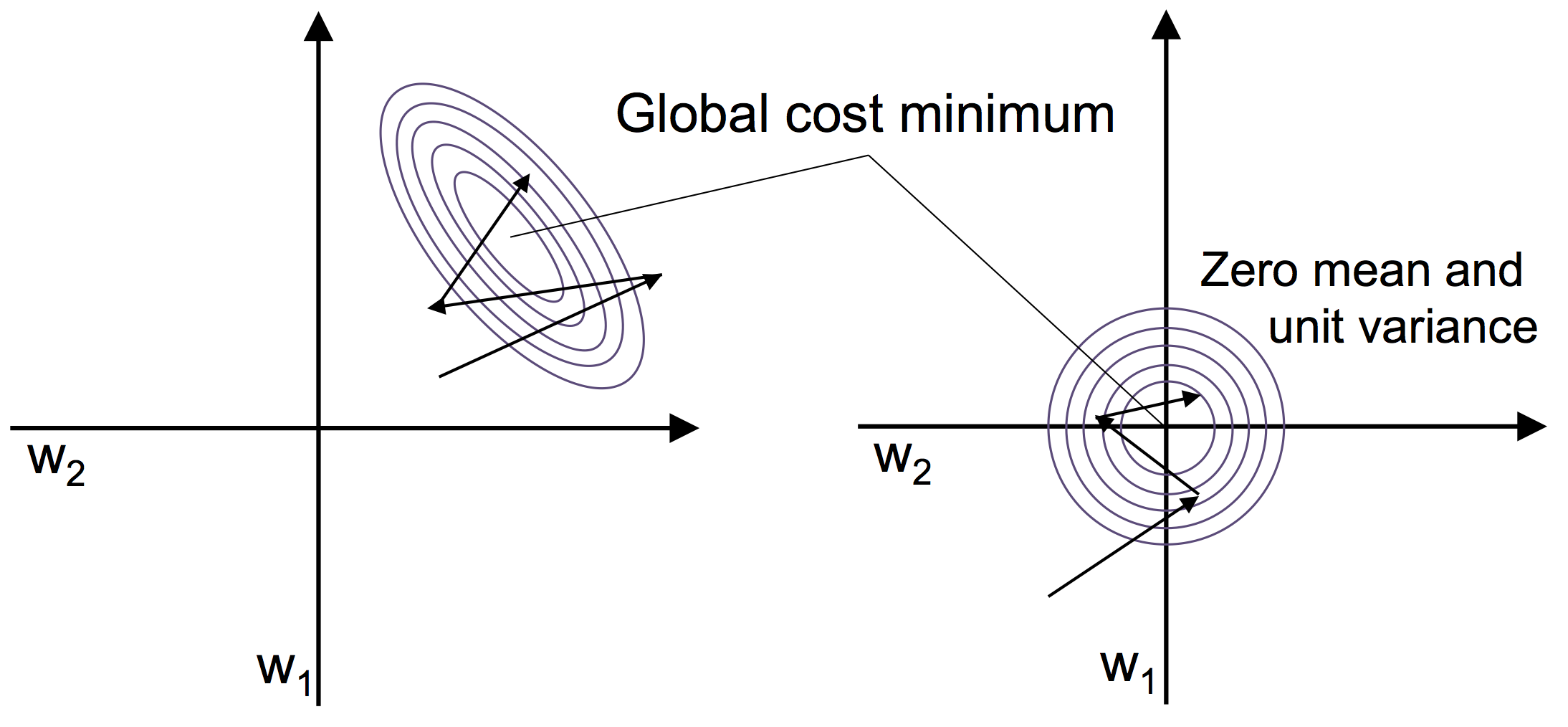
例如，对第 $j$ 个特征，只需要对每个训练样本减去样本均值 $\mu_j$ ，并除以标准差 $\sigma_j$ ：

$$\begin{align} x_j^{'} = {\frac {x_j - \mu_j} {\sigma_j}} \end{align}$$

标准化可以通过 NumPy 的方法轻松实现：

1
2
3
X_std = np.copy(X)
X_std[:, 0] = (X[:, 0] - X[:, 0].mean()) / X[:, 0].std()
X_std[:, 1] = (X[:, 1] - X[:, 1].mean()) / X[:, 1].std()

标准化后，再次使用 Adaline 进行训练，可以看到在学习率 $\eta = 0.01$ 上可以收敛：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
ada = AdalineGD(n_iter=15, eta=0.01)
ada.fit(X_std, y)

plot_decision_regions(X_std, y, classifier=ada)
plt.title('Adaline - Gradient Descent')
plt.xlabel('sepal length [standardized]')
plt.ylabel('petal length [standardized]')
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()

plt.plot(range(1, len(ada.cost_) + 1), ada.cost_, marker='o')
plt.xlabel('Epochs')
plt.ylabel('Sum-squared-error')

plt.tight_layout()
plt.show()

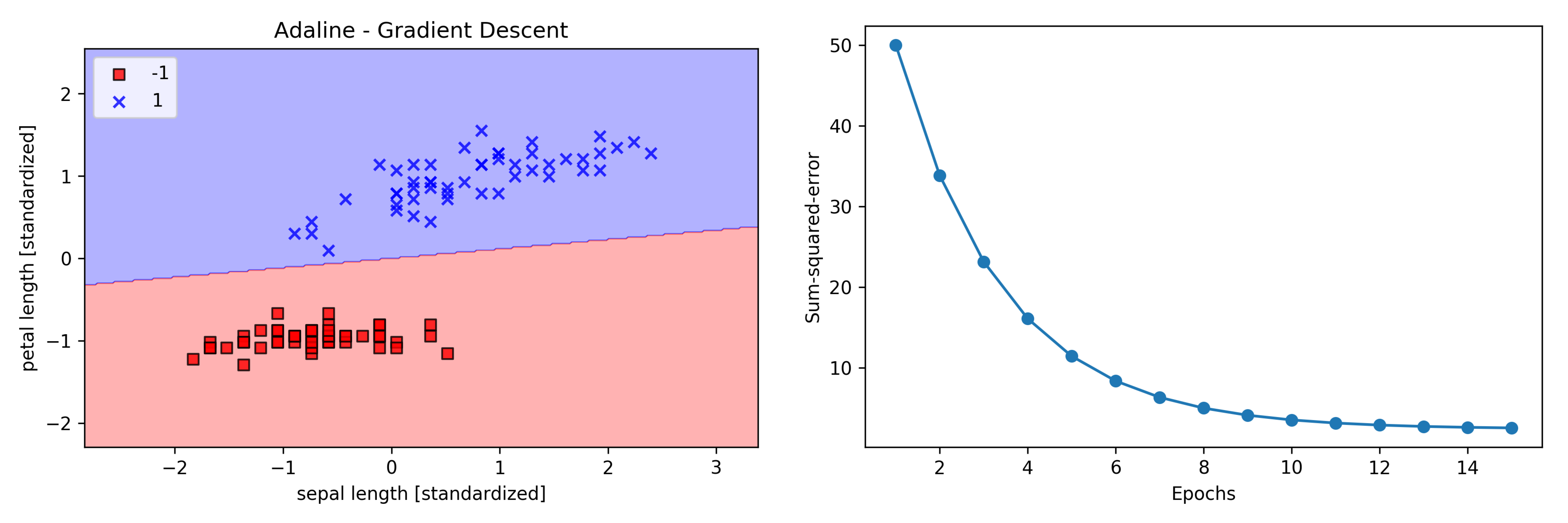
上图显示成本函数 SSE 随着训练次数的增加而逐渐变小，样本正确分类时，成本函数得到最小化，但并不为 0。

随机梯度下降法

批量梯度下降法在每次训练时，都需要使用到所有样本。假设有一个百万数量级的数据集（这在机器学习中并不罕见），使用批量梯度下降法会带来极大的计算成本，其权重的更新如下：

$$\begin{align} \Delta w = \eta {\Sigma_i(y^{(i)} - \phi(z^{(i)}))} x^{(i)} \end{align}$$

一种流行替代方法是随机梯度下降法（Stochastic Gradient Descent，SGD），有时也称为迭代（Iterative）梯度下降法或在线（On-line）梯度下降法，每次使用单个训练样本对权重进行更新：

$$\begin{align} \Delta w = \eta (y^{(i)} - \phi(z^{(i)})) x^{(i)} \end{align}$$

相对于批量梯度下下降法，随机梯度下降法的权重的更新频率更快，通常收敛也会更快。由于单个样本有很大的随机性（即噪音较大），每次迭代方向并不是都朝着局部最优解方向，算法准确率会相对下降一些。但随着训练次数增加，通常能够收敛到局部最优解附近。采用随机梯度下降法时，在每个训练时期都需要对样本进行洗牌，以获得随机样本。

在随机梯度下降法的实现中，固定学习率 $\eta$ 经常被随着时间的推移而减少的自适应学习率来代替，如 ${\frac {常数1} {迭代次数n_{iter} + 常数2}}$ 。

随机梯度下降法的另一个优点是在线学习（On-line Learning）。每当获取新的样本数据之后，都可以对模型进行训练。这能够适用于持续输入大量数据（如网络应用中的用户数据）的情况，另外每次训练后可以丢弃样本以防止数据累积造成的空间不足。

小批量梯度下降法（Mini-batch Gradient Descent，MBGD）是批量梯度下降法和随机梯度下降法思想的融合，每次训练采用小批量的样本（例如样本总数为 1000，每次训练采用其中随机 10 个），可以克制 BGD 训练较慢和 SGD 噪音较大的问题。

基于随机梯度下降法的 Adaline 实现

对上节的代码进行调整，添加权重的在线学习函数 partial_fit 、训练样本洗牌函数 _shuffle、权重初始化函数 _initialize_weights和权重调节函数 _update_weights ，实现基于随机梯度下降的 Adaline。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
import numpy as np


class AdalineSGD(object):
    def __init__(self, eta=0.01, n_iter=10, shuffle=True, random_state=None):
        self.eta = eta
        self.n_iter = n_iter
        self.w_initialized = False
        self.shuffle = shuffle
        self.random_state = random_state

    def fit(self, X, y):
        self._initialize_weights(X.shape[1])
        self.cost_ = []
        for i in range(self.n_iter):
            if self.shuffle:
                X, y = self._shuffle(X, y)
            cost = []
            for xi, target in zip(X, y):
                cost.append(self._update_weights(xi, target))
            avg_cost = sum(cost) / len(y)
            self.cost_.append(avg_cost)
        return self

    def partial_fit(self, X, y):
        if not self.w_initialized:
            self._initialize_weights(X.shape[1])
        if y.ravel().shape[0] > 1:
            for xi, target in zip(X, y):
                self._update_weights(xi, target)
        else:
            self._update_weights(X, y)
        return self

    def _shuffle(self, X, y):
        r = self.rgen.permutation(len(y))
        return X[r], y[r]

    def _initialize_weights(self, m):
        """Initialize weights to small random numbers"""
        self.rgen = np.random.RandomState(self.random_state)
        self.w_ = self.rgen.normal(loc=0.0, scale=0.01,
                                   size=1 + m)
        self.w_initialized = True

    def _update_weights(self, xi, target):
        output = self.activation(self.net_input(xi))
        error = (target - output)
        self.w_[1:] += self.eta * xi.dot(error)
        self.w_[0] += self.eta * error
        cost = 0.5 * error ** 2
        return cost

    def net_input(self, X):
        return np.dot(X, self.w_[1:]) + self.w_[0]

    def activation(self, X):
        return X

    def predict(self, X):
        return np.where(self.activation(self.net_input(X)) >= 0.0, 1, -1)

对算法训练过程进行绘图：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
ada = AdalineSGD(n_iter=15, eta=0.01, random_state=1)
ada.fit(X_std, y)

plot_decision_regions(X_std, y, classifier=ada)
plt.title('Adaline - Stochastic Gradient Descent')
plt.xlabel('sepal length [standardized]')
plt.ylabel('petal length [standardized]')
plt.legend(loc='upper left')

plt.tight_layout()
plt.show()

plt.plot(range(1, len(ada.cost_) + 1), ada.cost_, marker='o')
plt.xlabel('Epochs')
plt.ylabel('Average Cost')

plt.tight_layout()
plt.show()

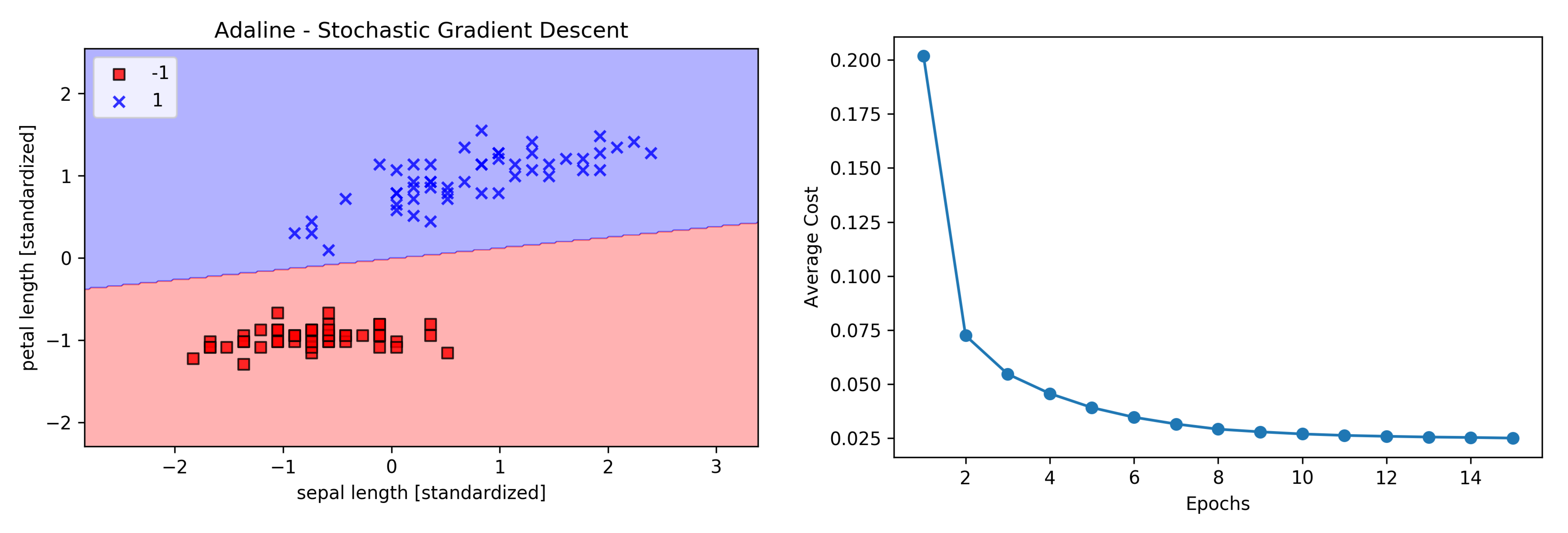
从上图可以看到，随机梯度下降法每次使用单个样本训练，成本函数 SSE 也可以很快下降，15个周期之后的决策边界与上节相似。
对于在线学习的场景，对单个样本调用 ada.partial_fit(X_std[0, :], y[0]) 即可对训练模型进行更新。